A circular disc of radius carries surface charge density =σ0(1−rR) , where σ0 is a constant and is the distance from the center of the disc Electric flux through a lange spherical surface that endcloses the charged disc completely is ϕ0. electric flux through another spherical surface of radius R4 and consentri with the disc is ϕ . Then the ratio ϕ0ϕ is __________.
The correct Answer is:6.4
To solve the problem, we need to find the ratio of the electric flux through a large spherical surface that encloses a charged disc completely (denoted as ϕ0) to the electric flux through another spherical surface of radius R/4 that is concentric with the disc (denoted as ϕ).
1. Understanding the Surface Charge Density:
The surface charge density on the disc is given by:
σ(r)=σ0(1−rR)
where r is the distance from the center of the disc and R is the radius of the disc.
2. Finding the Total Charge on the Disc:
To find the total charge Q on the disc, we need to integrate the charge density over the area of the disc. We can consider the disc as composed of infinitesimally thin rings:
- The area of an elemental ring at radius r and thickness dr is:
dA=2πrdr
- The charge dQ on this ring is:
dQ=σ(r)⋅dA=σ0(1−rR)⋅2πrdr
- Thus, the total charge Q on the disc is:
Q=∫R0dQ=∫R0σ0(1−rR)⋅2πrdr
3. Calculating the Integral:
- Expanding the integral:
Q=2πσ0∫R0(r−r2R)dr
- Evaluating the integral:
∫R0rdr=R22,∫R0r2dr=R33
- Therefore:
Q=2πσ0(R22−1R⋅R33)=2πσ0(R22−R23)=2πσ0⋅3R2−2R26=πσ0R23
4. Calculating Electric Flux ϕ0:
The electric flux through the large spherical surface that encloses the charged disc is given by Gauss's law:
ϕ0=Qϵ0=πσ0R23ϵ0
5. Calculating Electric Flux ϕ through the smaller sphere:
For the smaller sphere of radius R/4, we find the charge enclosed within this radius:
- The charge Q′ enclosed by the smaller sphere can be calculated similarly, but we integrate only up to R/4:
Q′=2πσ0∫R/40(1−rR)rdr
- Evaluating this integral gives:
Q′=2πσ0(∫R/40rdr−1R∫R/40r2dr)
- Carrying out the integrals, we find:
Q′=2πσ0((R/4)22−1R⋅(R/4)33)=2πσ0(R232−R2192)=2πσ0⋅6R2−R2192=10πσ0R2192
- Thus, the electric flux through the smaller sphere is:
ϕ=Q′ϵ0=10πσ0R2192ϵ0
6. Finding the Ratio ϕ0ϕ:
Now, we can find the ratio:
ϕ0ϕ=πσ0R23ϵ010πσ0R2192ϵ0=1310192=19230=325=6.4
Final Answer:
The ratio ϕ0ϕ is 6.4.
The surface charge density on the disc is given by:
σ(r)=σ0(1−rR)
where r is the distance from the center of the disc and R is the radius of the disc.
To find the total charge Q on the disc, we need to integrate the charge density over the area of the disc. We can consider the disc as composed of infinitesimally thin rings:
- The area of an elemental ring at radius r and thickness dr is:
dA=2πrdr
- The charge dQ on this ring is:
dQ=σ(r)⋅dA=σ0(1−rR)⋅2πrdr
- Thus, the total charge Q on the disc is:
Q=∫R0dQ=∫R0σ0(1−rR)⋅2πrdr
- Expanding the integral:
Q=2πσ0∫R0(r−r2R)dr
- Evaluating the integral:
∫R0rdr=R22,∫R0r2dr=R33
- Therefore:
Q=2πσ0(R22−1R⋅R33)=2πσ0(R22−R23)=2πσ0⋅3R2−2R26=πσ0R23
The electric flux through the large spherical surface that encloses the charged disc is given by Gauss's law:
ϕ0=Qϵ0=πσ0R23ϵ0
For the smaller sphere of radius R/4, we find the charge enclosed within this radius:
- The charge Q′ enclosed by the smaller sphere can be calculated similarly, but we integrate only up to R/4:
Q′=2πσ0∫R/40(1−rR)rdr
- Evaluating this integral gives:
Q′=2πσ0(∫R/40rdr−1R∫R/40r2dr)
- Carrying out the integrals, we find:
Q′=2πσ0((R/4)22−1R⋅(R/4)33)=2πσ0(R232−R2192)=2πσ0⋅6R2−R2192=10πσ0R2192
- Thus, the electric flux through the smaller sphere is:
ϕ=Q′ϵ0=10πσ0R2192ϵ0
Now, we can find the ratio:
ϕ0ϕ=πσ0R23ϵ010πσ0R2192ϵ0=1310192=19230=325=6.4
The ratio ϕ0ϕ is 6.4.
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-26videos
JEE ADVANCED 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PHYSICS SECTION - IV Matrix Match Type2videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2021EXERCISE - QUESTION38videos
JEE ADVANCED 2021
Similar Questions
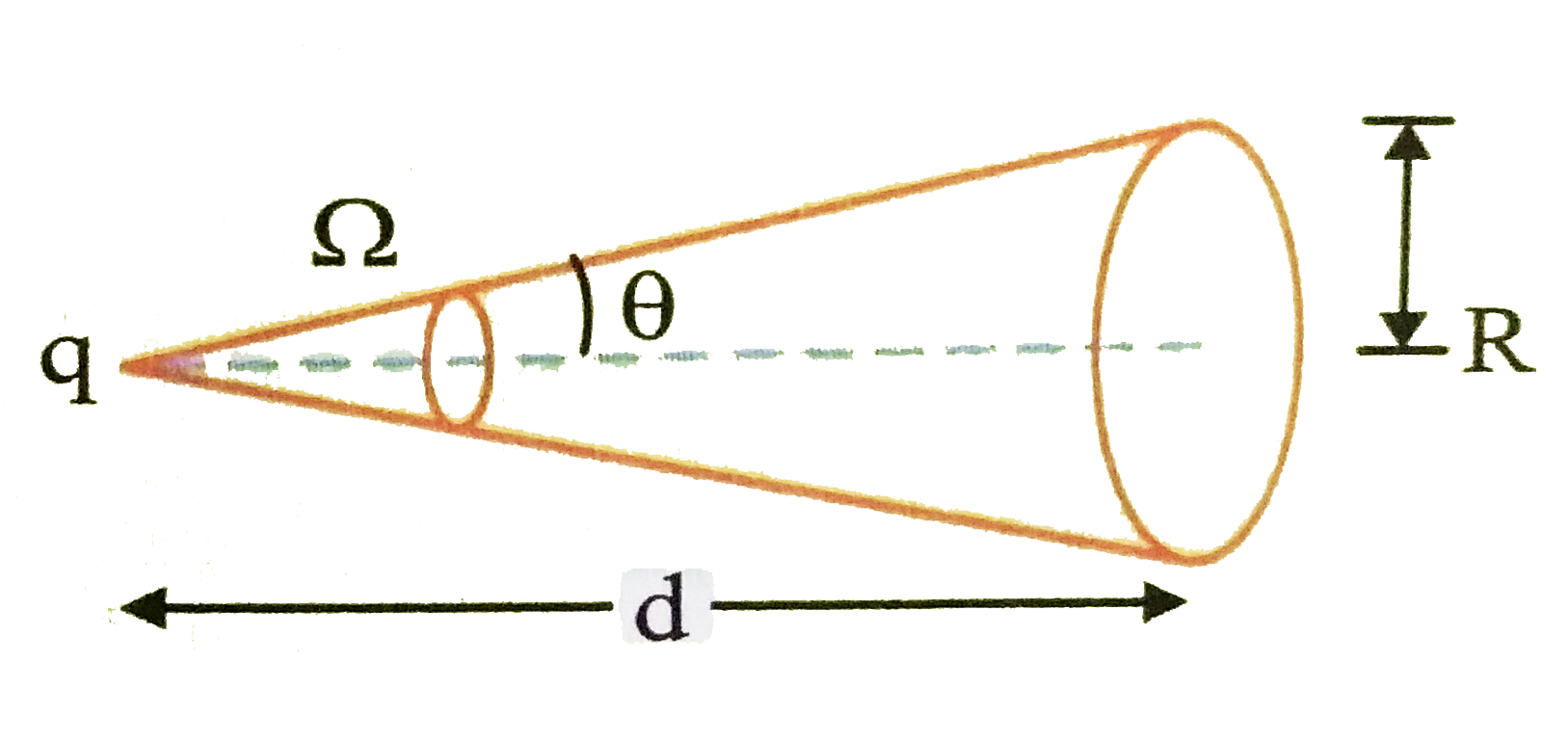
A point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
 View Solution
View SolutionA charge q is placed at the centre of a hollow sphere of radius r, Total electric flux passing through the spherical surface is __________
View Solution
Knowledge Check
- Question 1 - Select One
The electric flux through a closed surface area S enclosing charge Q is ϕ If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ - Question 2 - Select One
The electric flux through a chlosed surface area S enclosing charge Q is ϕ. If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ - Question 3 - Select One
An infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surfance of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surfce is .
 AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
AπR2σɛ0Bπ(R−x)2σɛ0Cπ(R−x)2σɛ0Dπ(R2−x2)σɛ0
A uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionA charge q is placed at the centre of a cylinder of radius R and length 2R. Then electric flux through the curved surface of the cylinder is
View SolutionIf the electric flux entering and leaving an enclosed surface are ϕ1andϕ2 respectively, then the electric charge present within the surface is
View SolutionIf the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
View SolutionIf the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2 then the electric charge inside the surface will he
View Solution

