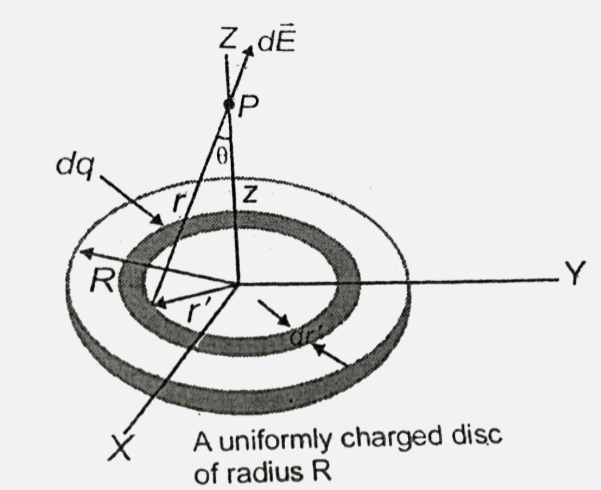
A uniformly charged disc of radius R having surface charge density is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
To find the electric field intensity along the z-axis at a distance z from the origin due to a uniformly charged disc of radius R with surface charge density σ, we can follow these steps:
1. Understand the Configuration:
- We have a uniformly charged disc lying in the xy-plane with its center at the origin. The disc has a radius R and a surface charge density σ.
2. Identify the Point of Interest:
- We want to find the electric field at a point P located on the z-axis at a distance z from the origin.
3. Consider an Elemental Ring:
- To calculate the electric field at point P, we can consider an elemental ring of radius r and thickness dr on the disc. The area of this ring is dA = 2πr dr.
4. Calculate the Charge on the Elemental Ring:
- The charge on this elemental ring can be expressed as:
dQ=σ⋅dA=σ⋅2πrdr
5. Determine the Electric Field Contribution from the Ring:
- The distance from the ring to point P is given by:
d=√r2+z2
- The electric field due to the charge dQ at point P has a magnitude given by Coulomb's law:
dE=14πϵ0dQd2=14πϵ0σ⋅2πrdrr2+z2
6. Resolve the Electric Field into Components:
- The electric field has both radial and axial components. Due to symmetry, the radial components will cancel out, and only the z-component will contribute to the net electric field at point P:
dEz=dE⋅cos(θ)=dE⋅z√r2+z2=14πϵ0σ⋅2πrdrr2+z2⋅z√r2+z2
7. Integrate to Find the Total Electric Field:
- The total electric field at point P is obtained by integrating dE_z from r = 0 to r = R:
Ez=∫R0dEz=∫R014πϵ0σ⋅2πrzdr(r2+z2)3/2
- This simplifies to:
Ez=σz2ϵ0∫R0rdr(r2+z2)3/2
8. Evaluate the Integral:
- The integral can be solved using substitution or standard integral formulas. The result of the integral is:
(−1√r2+z2)R0=−(1√R2+z2−1√0+z2)=1z−1√R2+z2
9. Final Expression for Electric Field:
- Substituting the result of the integral back into the expression for E_z gives:
Ez=σ2ϵ0(1−z√R2+z2)
Final Answer:
The electric field intensity along the z-axis at a distance z from the origin is given by:
Ez=σ2ϵ0(1−z√R2+z2)
- We have a uniformly charged disc lying in the xy-plane with its center at the origin. The disc has a radius R and a surface charge density σ.
- We want to find the electric field at a point P located on the z-axis at a distance z from the origin.
- To calculate the electric field at point P, we can consider an elemental ring of radius r and thickness dr on the disc. The area of this ring is dA = 2πr dr.
- The charge on this elemental ring can be expressed as:
dQ=σ⋅dA=σ⋅2πrdr
- The distance from the ring to point P is given by:
d=√r2+z2
- The electric field due to the charge dQ at point P has a magnitude given by Coulomb's law:
dE=14πϵ0dQd2=14πϵ0σ⋅2πrdrr2+z2
- The electric field has both radial and axial components. Due to symmetry, the radial components will cancel out, and only the z-component will contribute to the net electric field at point P:
dEz=dE⋅cos(θ)=dE⋅z√r2+z2=14πϵ0σ⋅2πrdrr2+z2⋅z√r2+z2
- The total electric field at point P is obtained by integrating dE_z from r = 0 to r = R:
Ez=∫R0dEz=∫R014πϵ0σ⋅2πrzdr(r2+z2)3/2
- This simplifies to:
Ez=σz2ϵ0∫R0rdr(r2+z2)3/2
- The integral can be solved using substitution or standard integral formulas. The result of the integral is:
(−1√r2+z2)R0=−(1√R2+z2−1√0+z2)=1z−1√R2+z2
- Substituting the result of the integral back into the expression for E_z gives:
Ez=σ2ϵ0(1−z√R2+z2)
The electric field intensity along the z-axis at a distance z from the origin is given by:
Ez=σ2ϵ0(1−z√R2+z2)
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A )
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B
20 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Knowledge Check
A uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
Aσ=F0ϕ0LBσ=F0ϕ0Cσ=F0Lϕ0Dσ=ϕ0F0A non conducting infinite rod is placed along the z−axis the upper half of the rod (lying along z≥0) is charged positively with a uniform linear charge density +λ, while the lower half (z<0) is charged negatively with a uniform linear charge density −λ. The origin is located at the junction of the positive and negative halves of the rod. A uniformly charged annular disc (surface charge density : σ0) of inner radius R and outer radius 2R is placed in the x−y plane with its centre at the origin. find the force on the rod due to the disc.
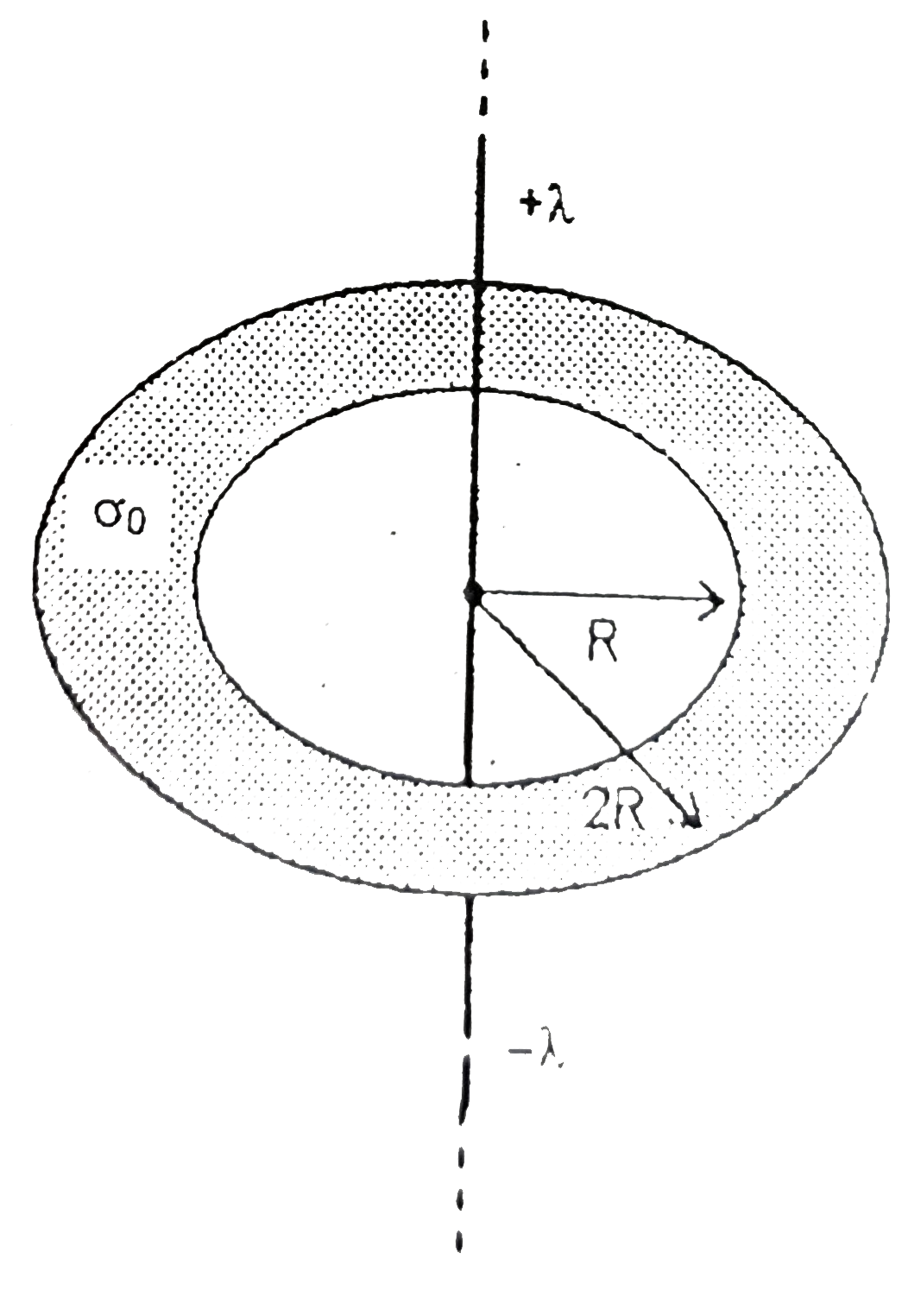 A2σ0λRε0Bσ0λR2ε0Cσ0λRε0Dσ0λR3ε0
A2σ0λRε0Bσ0λR2ε0Cσ0λRε0Dσ0λR3ε0A uniformly charged non conducting disc with surface charge density 10nC/m2 having radius R=3cm. Then find the value of electric field intensity at a point on the perpendicular bisector at a distance of r=2cm
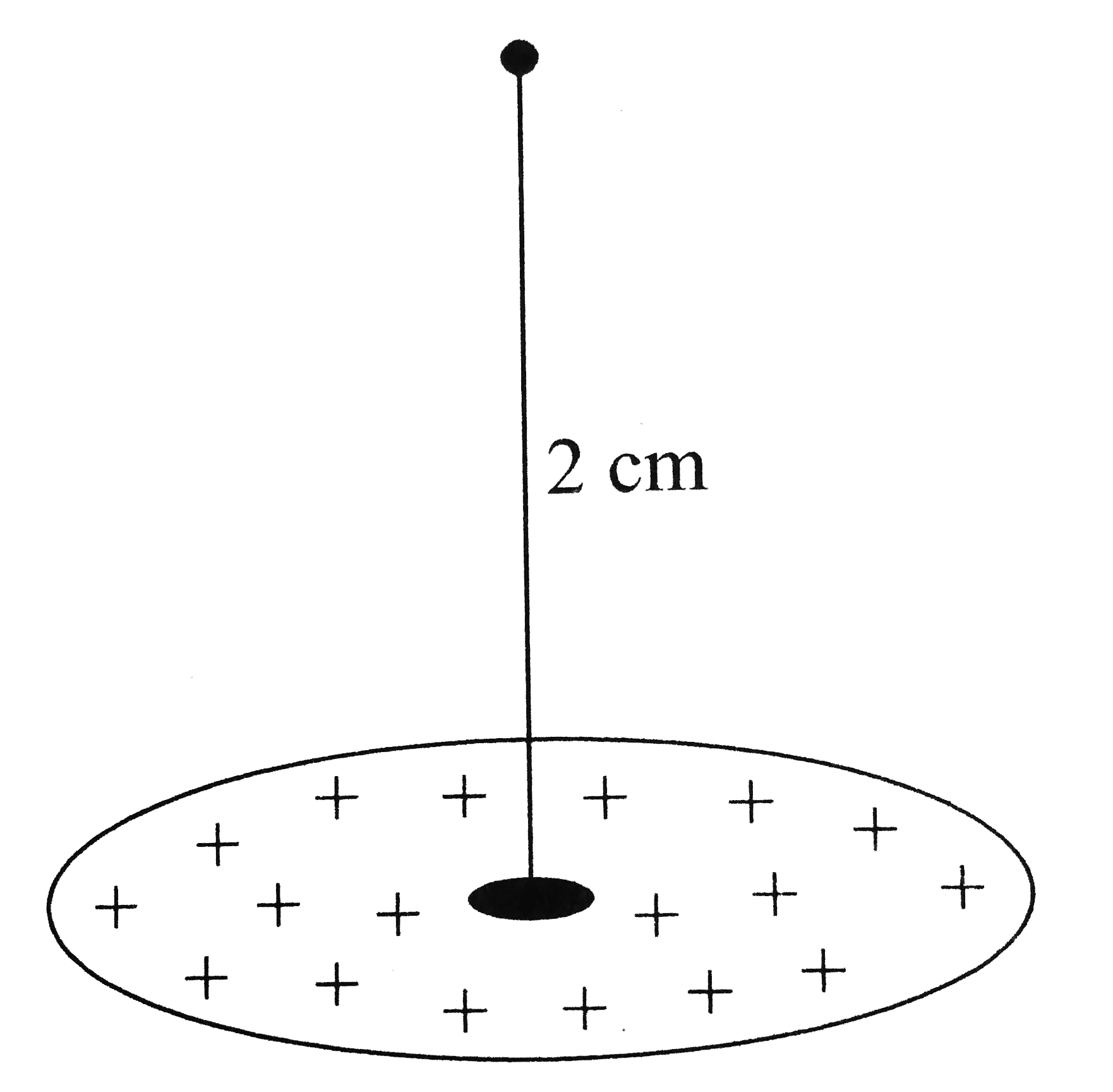 A348.6N/CB305.6N/CC251.2N/CD116.8N/C
A348.6N/CB305.6N/CC251.2N/CD116.8N/C
A very thin round plate of radius R carrying a uniform surface charge density σ is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l→0 and l>>R.
View SolutionA uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when R>>z.
Strategy : By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.
View SolutionA non-conducting infinite rod is placed along the 2 -axis, the upper half of the rod (lying along z≥0 ) is charged positively with a uniform linear charge density +λ while the lower half (z≤0) is charged negatively with a uniform linear charge density −λ. The origin is located at the junction of the positive and negative halves of the rod. A uniformly charged annular disc (surface charge density: σ0 ) of inner radius R and outer radius 2R is placed in the x−y plane with its center at the origin. The force on the rod due to the disc is yσ0λR8ɛ0, Find the value of y.
'(##CEN_KSR_PHY_JEE_C18_E01_037_Q22##)'
View SolutionConsider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View SolutionIf σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
View Solution
