A circular loop of radius r having N number of tunrns carries current I is placed in a placed in a uniform magnetic field→B parallel to the plane of the loop.The torque on the loop is : (A) NIπr2B (B) N2Iπr2B (C) NI2πr2B (D) NIπr2B2
To find the torque on a circular loop of radius r with N turns carrying a current I in a uniform magnetic field →B that is parallel to the plane of the loop, we can follow these steps:
Step 1: Understand the Torque Formula
The torque →τ on a current-carrying loop in a magnetic field is given by the formula:
→τ=→m×→B
where →m is the magnetic moment of the loop.
Step 2: Calculate the Magnetic Moment
The magnetic moment →m for a circular loop is given by:
→m=N⋅I⋅A^n
where A is the area of the loop and ^n is the unit vector perpendicular to the plane of the loop. For a circular loop, the area A is:
A=πr2
Thus, the magnetic moment becomes:
→m=N⋅I⋅πr2^n
Step 3: Determine the Direction of the Magnetic Moment
Assuming the loop lies in the xz-plane, the area vector ^n will point along the y-axis (using the right-hand rule). Therefore, we can express the magnetic moment as:
→m=N⋅I⋅πr2^j
Step 4: Express the Magnetic Field
The magnetic field →B is given to be parallel to the plane of the loop. Let's assume it is along the x-axis:
→B=B^i
Step 5: Calculate the Torque
Now, we can calculate the torque:
→τ=→m×→B=(N⋅I⋅πr2^j)×(B^i)
Using the cross product:
^j×^i=−^k
Thus, we have:
→τ=N⋅I⋅πr2⋅B(−^k)=−N⋅I⋅πr2⋅B^k
The negative sign indicates the direction of the torque, but we are interested in the magnitude:
|→τ|=N⋅I⋅πr2⋅B
Conclusion
The torque on the loop is:
|→τ|=N⋅I⋅πr2⋅B
Thus, the correct answer is option (A):
(A) NIπr2B
The torque →τ on a current-carrying loop in a magnetic field is given by the formula:
→τ=→m×→B
where →m is the magnetic moment of the loop.
The magnetic moment →m for a circular loop is given by:
→m=N⋅I⋅A^n
where A is the area of the loop and ^n is the unit vector perpendicular to the plane of the loop. For a circular loop, the area A is:
A=πr2
Thus, the magnetic moment becomes:
→m=N⋅I⋅πr2^n
Assuming the loop lies in the xz-plane, the area vector ^n will point along the y-axis (using the right-hand rule). Therefore, we can express the magnetic moment as:
→m=N⋅I⋅πr2^j
The magnetic field →B is given to be parallel to the plane of the loop. Let's assume it is along the x-axis:
→B=B^i
Now, we can calculate the torque:
→τ=→m×→B=(N⋅I⋅πr2^j)×(B^i)
Using the cross product:
^j×^i=−^k
Thus, we have:
→τ=N⋅I⋅πr2⋅B(−^k)=−N⋅I⋅πr2⋅B^k
The negative sign indicates the direction of the torque, but we are interested in the magnitude:
|→τ|=N⋅I⋅πr2⋅B
The torque on the loop is:
|→τ|=N⋅I⋅πr2⋅B
Thus, the correct answer is option (A):
(A) NIπr2B
Similar Questions
A triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
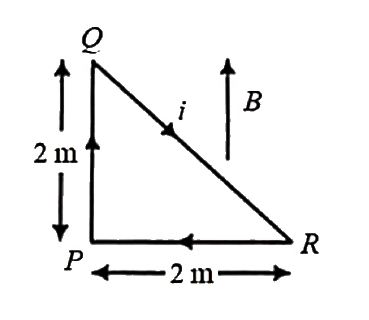
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA small circular flexible loop of wire of radius r carries a current I. It is placed in a uniform magnetic field B. The tension in the loop will be doubled if (Choose the incorrect option)
View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View Solution
