A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by

5cm
9cm
4.5cm
5.5cm
The correct Answer is:C
C1 is the centre of mass of cut portion and C2 that of remaining portion. We have to find x2
x1=14−10.5=3.5cm
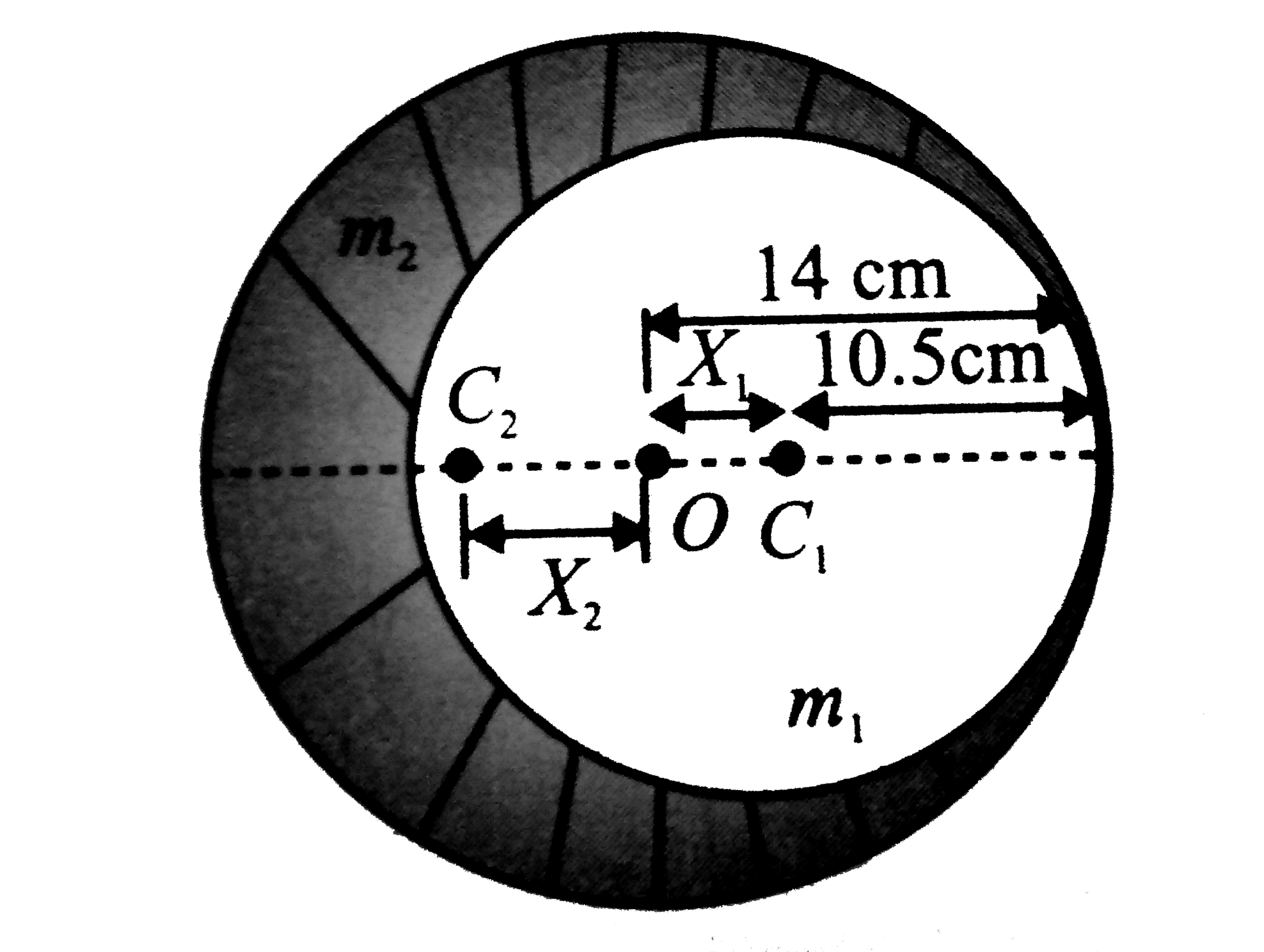
Mass will be proportional to area. So mass of the whole disc is
M=kπ(14)2
Mass of cut portion m1=kπ(10.5)2
Mass of the remaining portion m2=M−m1−kπ(142−10.52)
=kπ(24.5)×(3.6)
Now m1x1=m2x2
⇒x2=m1x1m2=(kπ(10.5)2×3.5)kπ(24.5)×3.5=4.5cm
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View Solution
Knowledge Check
A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
A uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
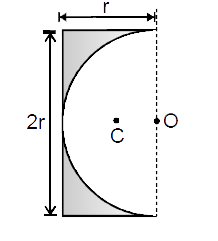
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
View SolutionFrom a uniform circular disc of diameter D, a circular disc or hole of diameter D/6 and having its centre at a distance of D/4 from the centre of the disc is scopped out. Determine the centre of mass of the remaining portion.
View SolutionFind the position of centre of mass of the T-shaped plate from O, in Fig.

View SolutionLocate the position of centre of mass of a uniform plate of Mass m as shown in fig 4E 34

View SolutionFrom a uniform circular plate of radius R, a small circular plate of radius R/4 is cut off as shown. If O is the center of the complete plate, then the x coordinate of the new center of mass of the remaining plate will be: X o Y
View SolutionFrom a uniform circular disc of diameter d,a circular disc of diameter d/6 and having centre at a distance d/4 from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
View Solution
