A circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
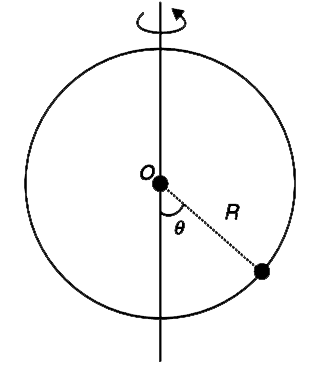
The correct Answer is:T=2π√Rcosθg
Step by step video, text & image solution for A circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle theta with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
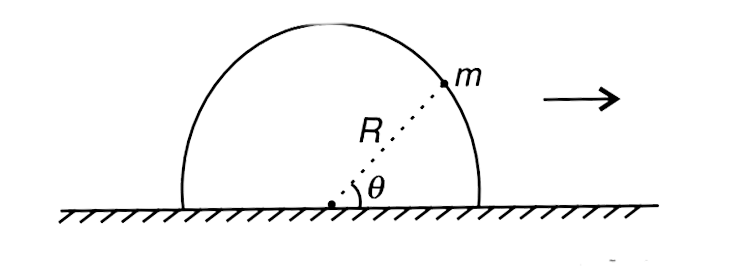
A semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
View SolutionA thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
View Solution
Knowledge Check
A circular are (AB) of thin wire frame of radius R and mass M makes an angle of 90∘ at the origin.The centre of mass of the arc lies at
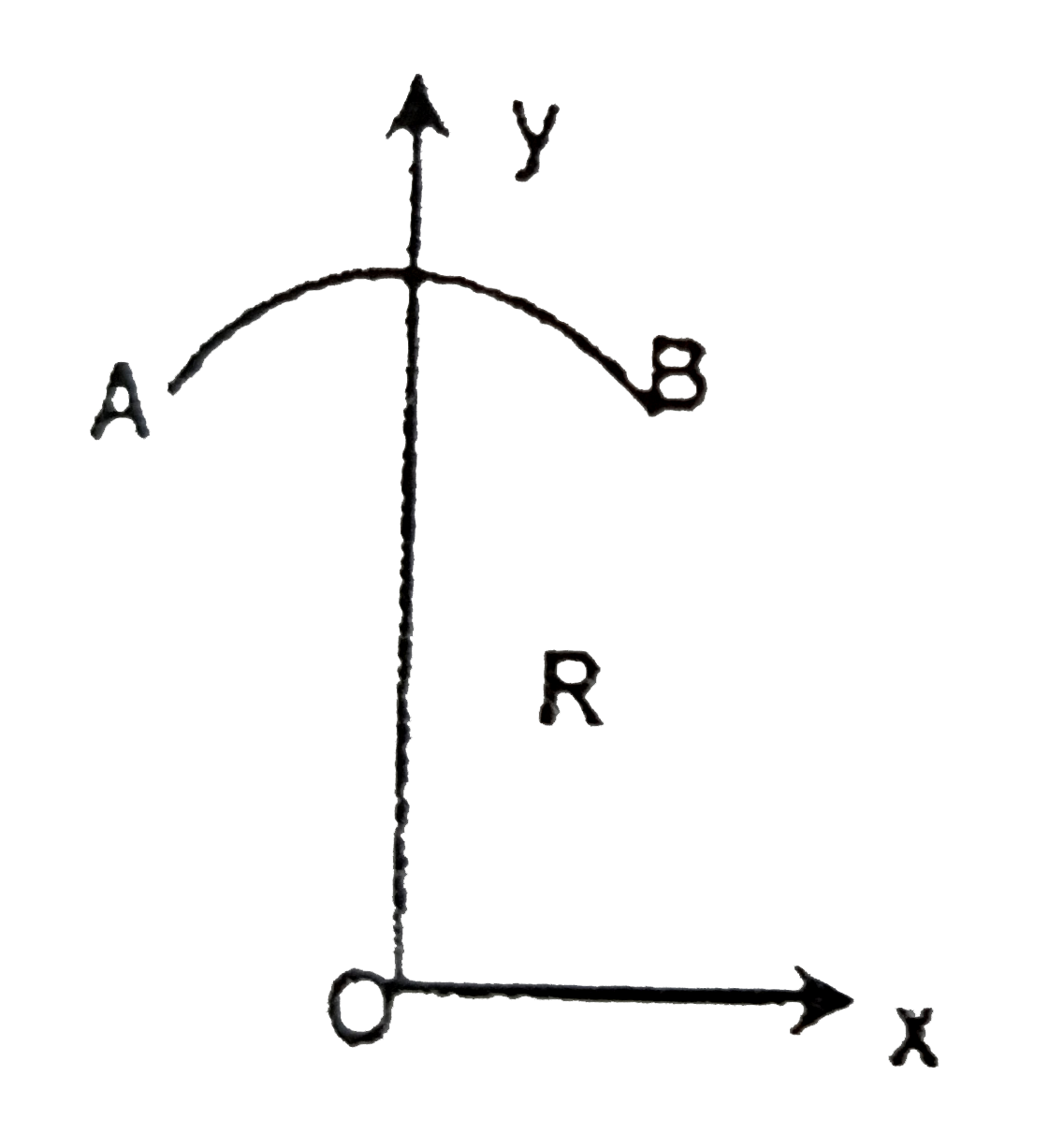 A[0,(2/π)R]B[0,(√2/π)R]C[0,(2√2/π)R]D[0,(4/π)R]
A[0,(2/π)R]B[0,(√2/π)R]C[0,(2√2/π)R]D[0,(4/π)R]A bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
A√2gRB√2gR(1−sinθ)C√2gR(1−cosθ)D2√gRA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
A√2grB√2gr(1−sinθ)C√2gr(1−cosθ)D2√gr

A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View SolutionA stone of mass m tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is Y, Then the increase in the length of the wire is
View SolutionA semicircular wire of radius R is oriented vertically. A small bead is released from rest from the top of the wire. It slides without friction under the influence of gravity to the bottom, where it then leaves the wire horizontally and falls distance H to the ground. The bead lands a horizontal distance D away from where it was launched. Which of the following is correct graph of RH vetsus D2?
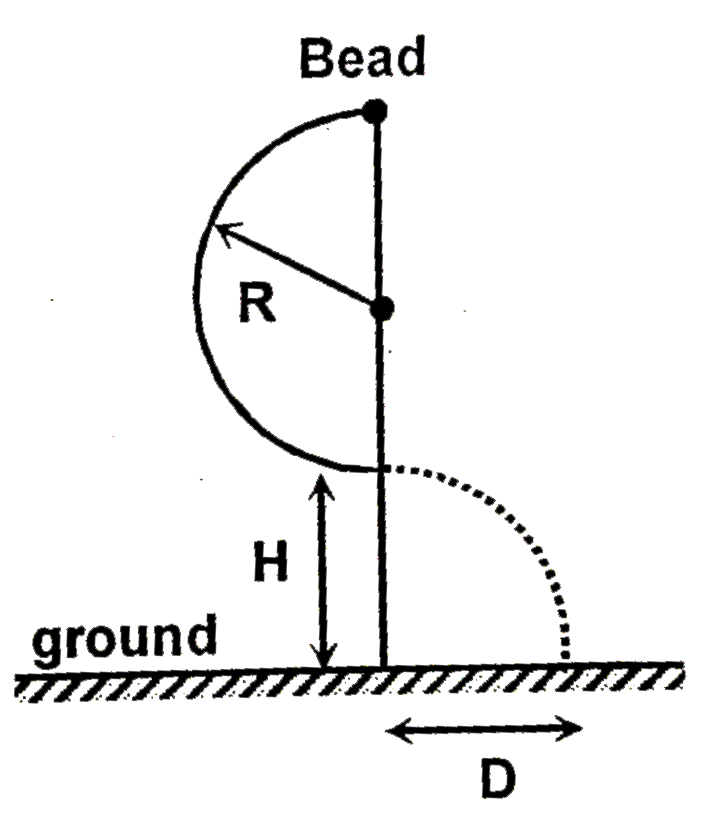
View SolutionA semicircular wire of radius R is oriented vertically. A small bead is released from rest at the top of the wire, it slides without friction under the influence of gravity to the bottom, where is then leaves the wire horizontally and falls a distance H to the ground. The bead lands a horizontal distance D away from where it was launched.
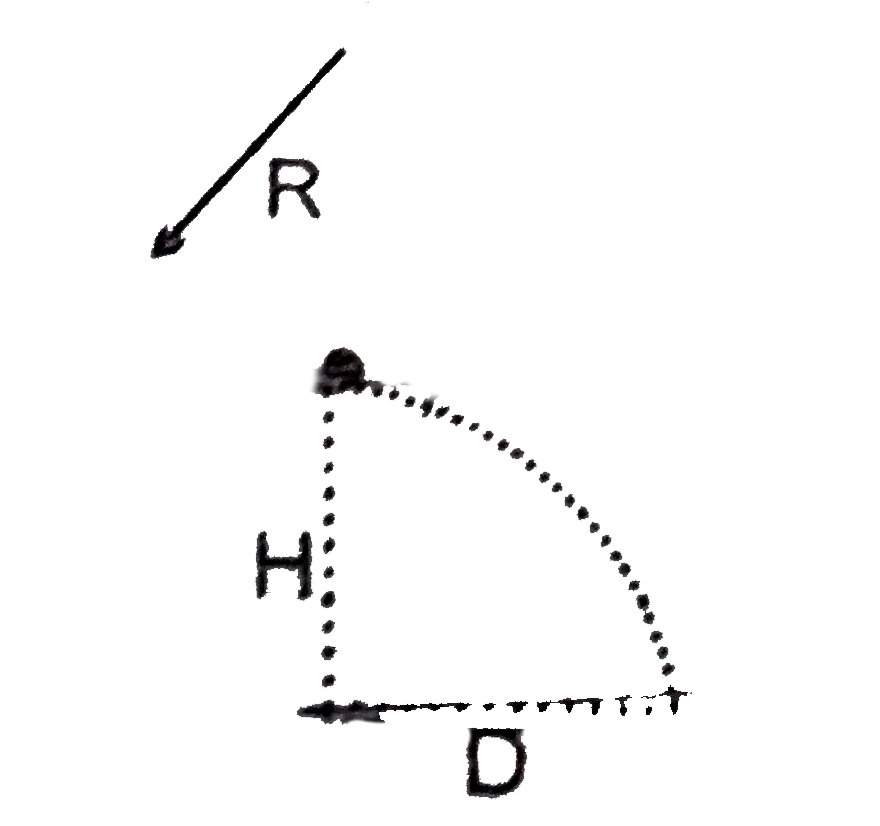
Which of the following is a correct graph of RH against D2 ?
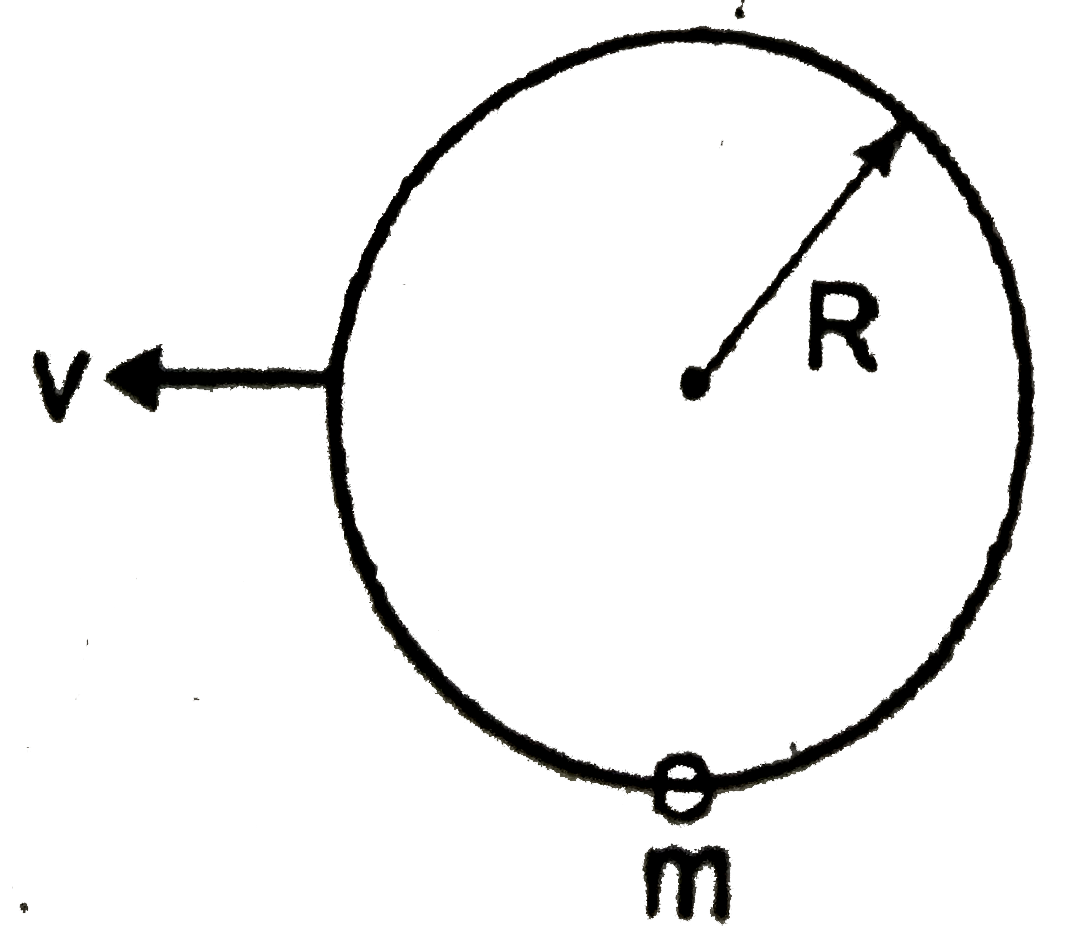
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
View Solution
