A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
zero
To find the induced electromotive force (e.m.f.) in a circular wire of radius r that rotates about its own axis with angular speed ω in a magnetic field B that is perpendicular to its plane, we can follow these steps:
Step 1: Understanding the Setup
We have a circular wire of radius r rotating about its own axis. The magnetic field B is perpendicular to the plane of the wire.
Step 2: Determine the Area Swept by the Wire
As the wire rotates, it sweeps out an area. The area A of the circular wire is given by:
A=πr2
Step 3: Calculate the Rate of Change of Area
The wire rotates with an angular speed ω. The rate at which the area is swept out (which is related to the change in magnetic flux) can be expressed as:
dAdt=ωA=ω(πr2)
Step 4: Calculate the Magnetic Flux
The magnetic flux Φ through the wire is given by:
Φ=B⋅A
Substituting the area A:
Φ=B⋅(πr2)
Step 5: Induced EMF Calculation
According to Faraday's law of electromagnetic induction, the induced e.m.f. E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux:
E=−ddt(B⋅πr2)
Since B and r are constants, we have:
E=−B⋅ddt(πr2)=−B⋅πr2⋅dωdt
However, since the area is constant and does not change with time, the induced e.m.f. is actually zero:
E=0
Final Answer
The induced e.m.f. in the circular wire rotating in a magnetic field perpendicular to its plane is:
E=0
We have a circular wire of radius r rotating about its own axis. The magnetic field B is perpendicular to the plane of the wire.
As the wire rotates, it sweeps out an area. The area A of the circular wire is given by:
A=πr2
The wire rotates with an angular speed ω. The rate at which the area is swept out (which is related to the change in magnetic flux) can be expressed as:
dAdt=ωA=ω(πr2)
The magnetic flux Φ through the wire is given by:
Φ=B⋅A
Substituting the area A:
Φ=B⋅(πr2)
According to Faraday's law of electromagnetic induction, the induced e.m.f. E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux:
E=−ddt(B⋅πr2)
Since B and r are constants, we have:
E=−B⋅ddt(πr2)=−B⋅πr2⋅dωdt
However, since the area is constant and does not change with time, the induced e.m.f. is actually zero:
E=0
The induced e.m.f. in the circular wire rotating in a magnetic field perpendicular to its plane is:
E=0
Topper's Solved these Questions
Similar Questions
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
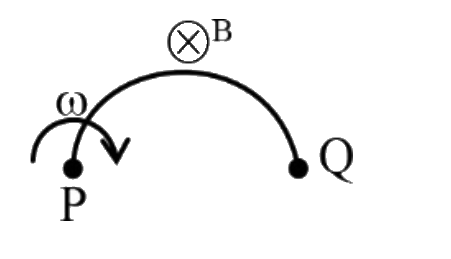
View Solution
Knowledge Check
A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
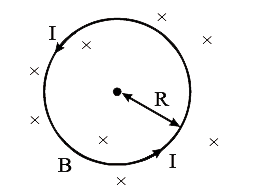 ABIRB2πBIRCπBIRD2BIR
ABIRB2πBIRCπBIRD2BIRA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A circular disc is rotating about its own axis, the direction of its angular momentum is
AradialBalong axis of rotationCalong tangentDperpendicular to the direction of angular velocity
A wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
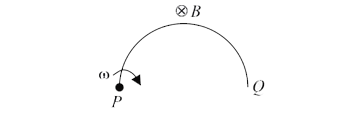
View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionA copper disc of radius 1m is rotated about its natural axis with an angular velocity 2rad/sec in a uniform magnetic field 5 telsa with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA metal disc of radius R rotates with an angular velcoity ω about an axis perpendicular to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is

View Solution
