A closed hollow insulated cylinder is filled with gas at 0∘C and also contains an insulated piston of negligible weight and negligible thickness at the middle point. The gas on one side of the piston is heated to 100∘C. If the piston moves 5cm the length of the hollow cylinder is
13.65cm
27.3cm
38.6cm
64.6cm
The correct Answer is:D
To solve the problem, we need to analyze the situation involving the closed hollow insulated cylinder with an insulated piston. We will use the ideal gas law and the concept of thermal equilibrium to find the length of the cylinder.
1. Understanding the Initial Conditions:
- The gas in the cylinder is initially at 0∘C, which is 273K.
- The piston divides the cylinder into two equal parts, each with volume V=A⋅L2, where A is the cross-sectional area and L is the total length of the cylinder.
2. Heating One Side of the Cylinder:
- The gas on one side of the piston is heated to 100∘C, which is 373K.
- The other side remains at 0∘C (273K) because the walls are insulated.
3. Movement of the Piston:
- The piston moves 5cm (or 0.05m) towards the side that was heated.
- After the piston moves, the volume on the heated side becomes V1=A(L2+0.05).
- The volume on the cooler side becomes V2=A(L2−0.05).
4. Applying the Ideal Gas Law:
- According to the ideal gas law, for both sides of the piston, we have:
V1T1=V2T2
- Here, T1=373K and T2=273K.
5. Substituting the Volumes:
- Substitute the expressions for V1 and V2:
A(L2+0.05)373=A(L2−0.05)273
- The area A cancels out:
L2+0.05373=L2−0.05273
6. Cross-Multiplying to Solve for L:
- Cross-multiply to eliminate the fractions:
273(L2+0.05)=373(L2−0.05)
- Expanding both sides:
273⋅L2+13.65=373⋅L2−18.65
7. Rearranging the Equation:
- Rearranging gives:
273⋅L2−373⋅L2=−18.65−13.65
- Simplifying:
−100⋅L2=−32.3
- Thus:
L2=32.3100⟹L=32.3⋅2100=64.6 cm
Final Answer:
The length of the hollow cylinder is 64.6 cm.
- The gas in the cylinder is initially at 0∘C, which is 273K.
- The piston divides the cylinder into two equal parts, each with volume V=A⋅L2, where A is the cross-sectional area and L is the total length of the cylinder.
- The gas on one side of the piston is heated to 100∘C, which is 373K.
- The other side remains at 0∘C (273K) because the walls are insulated.
- The piston moves 5cm (or 0.05m) towards the side that was heated.
- After the piston moves, the volume on the heated side becomes V1=A(L2+0.05).
- The volume on the cooler side becomes V2=A(L2−0.05).
- According to the ideal gas law, for both sides of the piston, we have:
V1T1=V2T2
- Here, T1=373K and T2=273K.
- Substitute the expressions for V1 and V2:
A(L2+0.05)373=A(L2−0.05)273
- The area A cancels out:
L2+0.05373=L2−0.05273
- Cross-multiply to eliminate the fractions:
273(L2+0.05)=373(L2−0.05)
- Expanding both sides:
273⋅L2+13.65=373⋅L2−18.65
- Rearranging gives:
273⋅L2−373⋅L2=−18.65−13.65
- Simplifying:
−100⋅L2=−32.3
- Thus:
L2=32.3100⟹L=32.3⋅2100=64.6 cm
The length of the hollow cylinder is 64.6 cm.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - First Law Of Thermodynamics , Internal Energy And Work Done
55 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Application Of First Law Of Thermodynamics In Different Situations
25 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
Similar Questions
A uniform tube closed at both ends with a light piston in the middle contains a gas at 27∘C .If one part is heated to 127∘C the piston moves by 10cm .Then the length of the tube containing gas at higher temperature is
View SolutionA masslesss piston divides a closed thermallyy insulated cylinder into two equal parts. One part contains M = 28 g of nitrogen. At this temperature, one-third of molecules are dissociated into atoms and the other part is evacuated. The piston is released and the gas fills the whole volume of the cylinder at temperature T0. Then, the piston is slowly displaced back to its initial position. calculate the increases in internal energy of the gas. Neglect further dissociation of molecules during, the motion of the piston.
View Solution
Knowledge Check
A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l1, and that below the piston is l2, such that l1>l2. Each part of the cylinder contains n moles of an ideal gas at equal temeprature T. If the pistion is stationary, its mass, m, will be given by : (R is universal gas constant and g is the acceleration due to gravitey)
ARTng[l1−3l2l1l2]BRTg[2l1+l2l1l2]CnRTg[1l2+1l1]DnRTg[l1−l2l1l2]A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l1, and that below the piston is l2, such that l1>l2. Each part of the cylinder contains n moles of an ideal gas at equal temeprature T. If the pistion is stationary, its mass, m, will be given by : (R is universal gas constant and g is the acceleration due to gravitey)
ARTng[l1−3l2l1l2]BRTg[2l1+l2l1l2]CnRTg[1l2+1l1]DnRTg[l1−l2l1l2]A gas is filled in the cylinder shown in fig. The two pistons are joined by a string. If the gas is heated, the right piston will
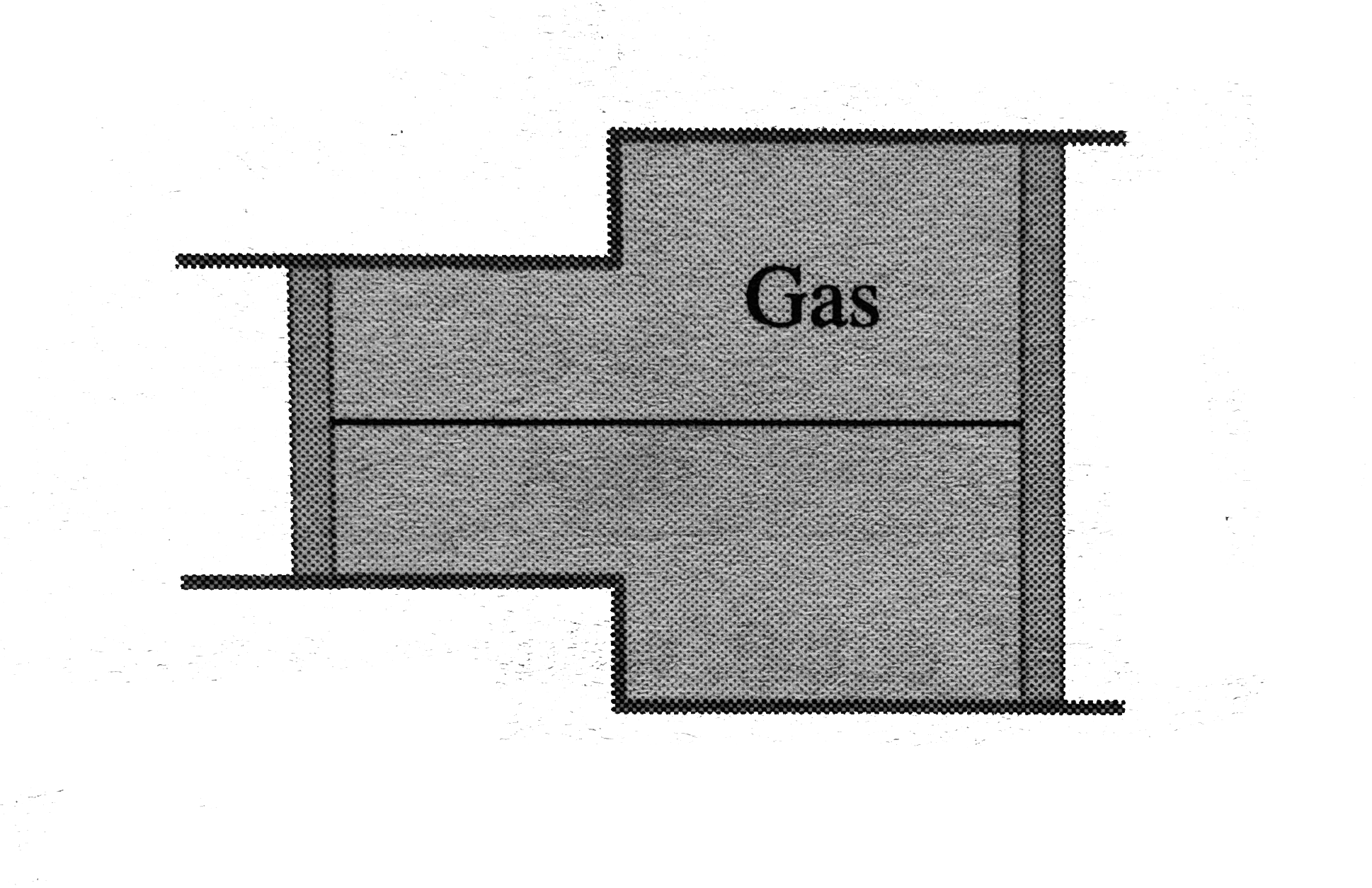 Amove toward leftBmove toward rightCremain stationaryDnone of these
Amove toward leftBmove toward rightCremain stationaryDnone of these
A weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.
View SolutionIn a cylindrical container two pistons enclose gas in two compartments as shown in the figure. The pistons have negligible thickness and can move without friction. The sys- tem is originally in equilibrium. The outer piston is slowly moved out by 10 cm and the inner piston is found to move by 4 cm. Find the distance of the inner piston in equilibrium from the closed end of the cylinder if the outer piston is slowly moved out of the cylinder. Assume temperature of the gas to remain constant.
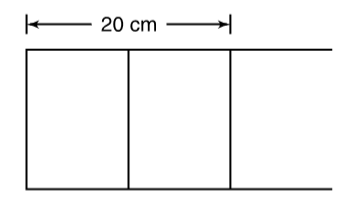
View Solution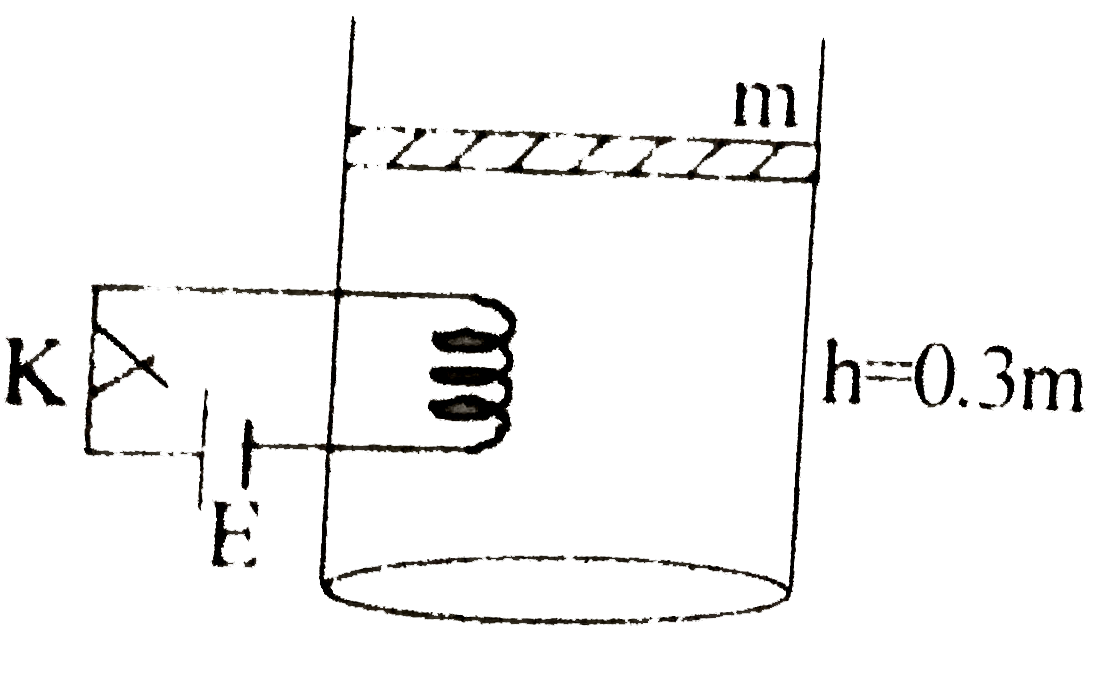
An insulated cylinder contains nitrogen gas which is sealed on the top by a heavy metal piston of mass m. piston is free to move with negligible friction, initial height of the piston is 0.3 m at temperature 27∘C when it is givenn some heat with the help of an electrical circuit piston slowly rises to height 0.5 m above the bottom of the cylinder. During expansion of te gas, net heat absorbed by the nitrogen gas:
View SolutionA vertical cylinder with heat-conducting walls is closed at the bottom and is fitted with a smooth light piston. It contains one mole of an ideal gas. The temperature of the gas is always equal to the surrounding\s temperature,T0, The piston is moved up slowly to increase the volume of the gas to η times. Which of the following is incorrect ?
View SolutionA vertical cylinder with heat - conducting walls is closed at the bottom and is fitted with a smooth light piston. It contains one mole of an ideal gas. The temperature of the gas is always equal to the surrounding 's temperature, T0 The piston is moved up slowly to increase the volume of the gas to η times. Which of the following is incorrect?
View Solution
