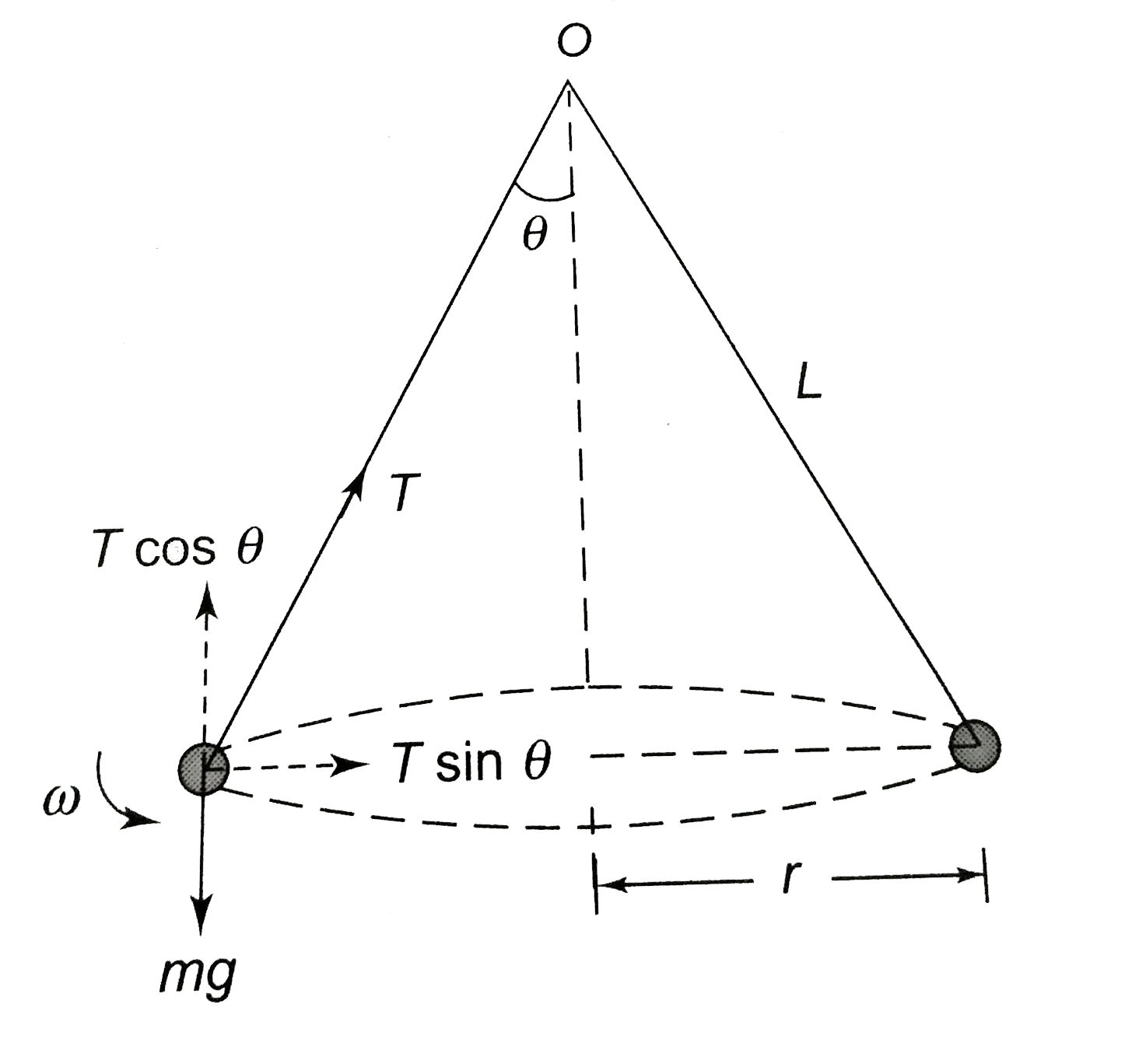
A coical pendulum consists of a string of length L whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed ω such that the string makes a constant angle θ with the verticle. calculate time period T0 of revolution of bob in terms of L,g and θ.
Time period of revolution T−(0)=2πω
Tcosθ=mg⇒T=mgcosθ
Tsinθ=mω2r
mgcosθsinθ=mω2Lsinθ(sincesinθ=rL)
ω2=gLcosθ⇒ω=√gLcosθ
Time period T0=2πω=2π√Lcosθg
Topper's Solved these Questions
Similar Questions
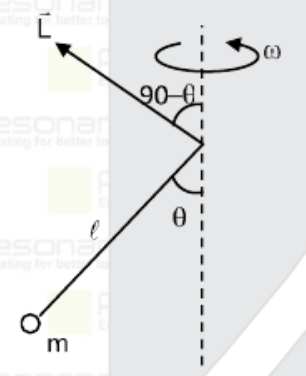
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionA stone tied to an inextensible string of length l=1m is kept horizontal. If it is released, find the angular speed of the stone when the string makes an angle θ=30∘ with horizontal.
View Solution
Knowledge Check
A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibriumA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.
A simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA small brass bob is revolving in a horizontal circle with a constant speed of 2ms−1 at the end of a string of length 1 m. Find the time required for one revolution of the body. What angle does the string make with the vertical ?
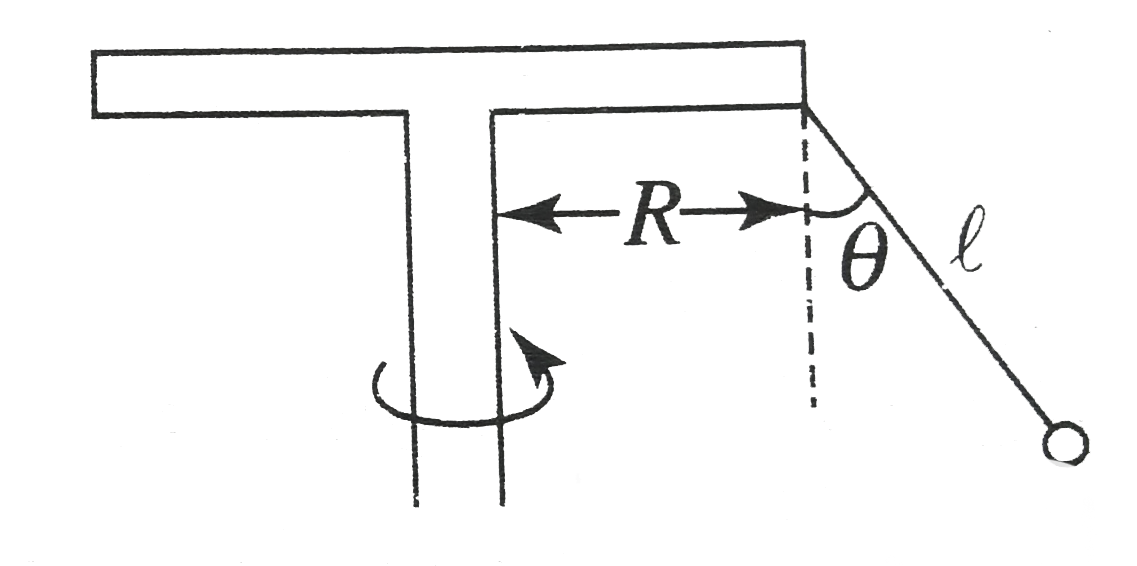
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
View SolutionA stone tied to the end of string 100cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 22s, then the acceleration of the stone is
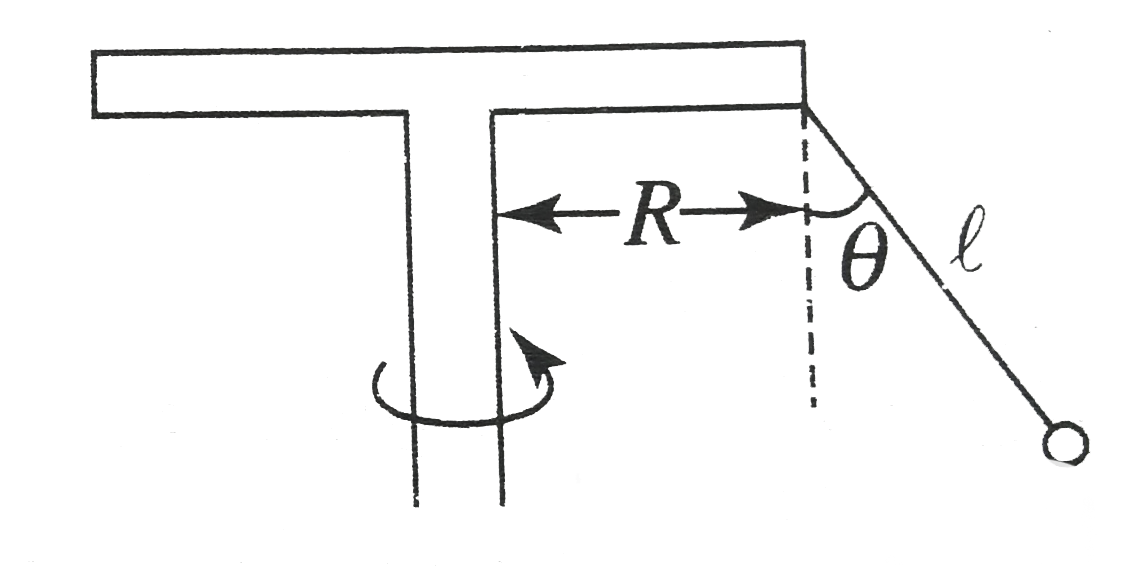
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
View Solution
