A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation 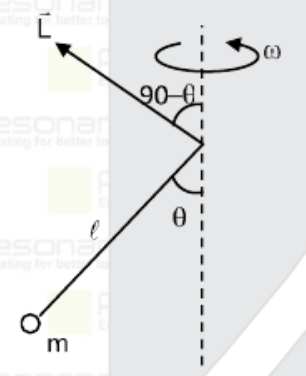
ml2ωsin2(θ)
2ml2ωsin2(θ)
ml2ωcos2(θ)
2ml2ωcos2(θ)
Step by step video & image solution for A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed omega and string makes an angle of theta with the vertical. Find the angular momentum of bob about axis of rotation by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A stone tied to an inextensible string of length l=1m is kept horizontal. If it is released, find the angular speed of the stone when the string makes an angle θ=30∘ with horizontal.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
Knowledge Check
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)A smalll bob attached to a string of length l is suspended from a rigid support and rotates with uniform speed along a circle in a horizontal plane. Let θ be the angle made by the string with the vertical, then the length of a simple pendulum having the same period is
Al/cosθBlsinθCl/sinθDlcosθ
A coical pendulum consists of a string of length L whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed ω such that the string makes a constant angle θ with the verticle. calculate time period T0 of revolution of bob in terms of L,g and θ.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle tˆa=37∘ with the vertical. Find the acceleration of the trolley.

View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
