A coil carrying a steady current is short-circuited. The current in it decreases $α$ times in time $t_{0}$ . The time constant of the circuit is

A

$τ = t_{0}$ In $α$

B

$τ = \frac{t_{0}}{I n α}$

C

$τ = \frac{t_{0}}{α}$

D

$τ = \frac{t_{0}}{α - 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$I = \frac{I_{0}}{α}$ at $t = t_{0}$
Since $I = I_{0} e_{0}^{- t_{0} / τ} \Rightarrow \frac{1}{α} = e_{0}^{- t_{0} / τ}$
$α = e_{0}^{- t_{0} / τ} \Rightarrow t_{0} = τ {log}_{e} α$
$τ = \frac{t_{0}}{{log}_{e} α}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider the circuit shown below. When switch $S_{1}$ is closed, let I be the current at time t, then applying Kirchhoff's law
$E - i R - L \frac{d i}{d t} = 0 or \int_{0}^{i} \frac{d i}{E - i R} = \frac{1}{L} \int_{0}^{1} d t$
$i = \frac{E}{R} (1 - e^{- \frac{R}{l} \cdot t})$
$\frac{L}{R}$ = time constant of circuit
When current reaches its steady value $(= i_{0}$ , open $S_{1}$ and close $S_{2}$ , the current does reach to zero finally but decays expnentially. The decay equation is given as $i = i_{0} e^{- \frac{R}{L} \cdot T}$ ).

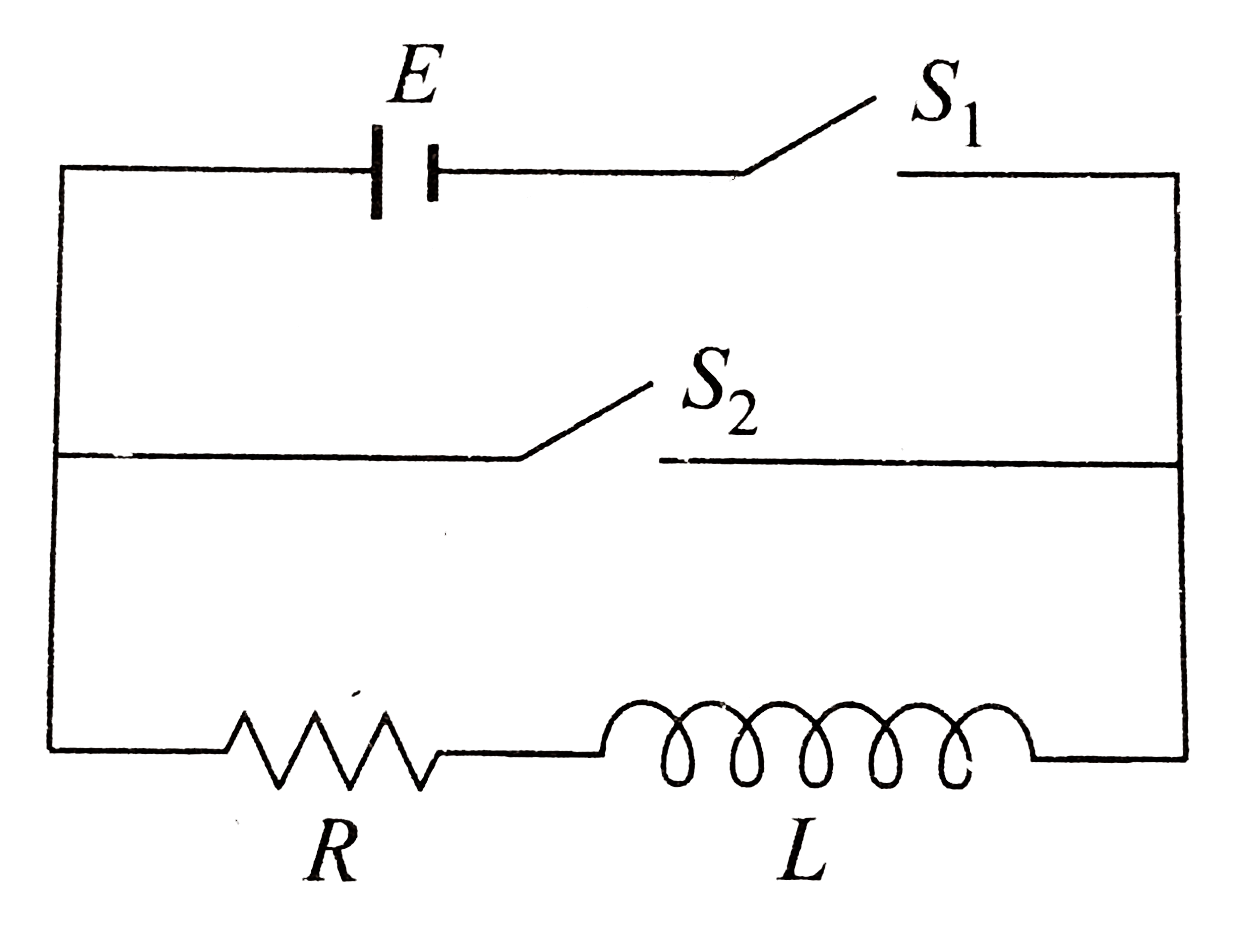
When a coil carrying a steady current is short circuited, the current decreases in it $η$ times in time $t_{0}$ . The time constant of the circuit is
A $t_{0} 1 n η$
B $\frac{t_{0}}{1 n η}$
C $\frac{t_{0}}{η}$
D $\frac{t_{0}}{η} - 1$
Question 2 - Select One
When a choke coil carrying a steady current is short circuited, the current in it decreases to $β (< 1)$ times its initial value in a time $T$ . The time constant of the choke coil is
A $\frac{T}{β}$
B $\frac{T}{ln (\frac{1}{β})}$
C $\frac{T}{ln β}$
D $T ln β$
Question 3 - Select One
At the time of short-circuit, the current in the circuit:
A(a) reduces substantially
B(b) does not change
C(c) increases heavily
D(d) varies continuously.

CENGAGE PHYSICS-INDUCTANCE-Exercises (single Correct )

Home
Ask Doubt
Profile