A coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
The equatio of the circuit is (I is the current )
LdIdt=RI=Vmcosωt
From the theory of different equations.
I=Ip+IC
where Ip is a particular integral and IC is the complementary function ( Solution of the differential equation with the RHS =0).Now
IC=ICOe−tR/L
and for Ip we write Ip=Imcos(ωt−φ)
Substituting we get
Im=Vm√R2+ω2L2,φ=tan−1(ωL)R
Then Im=Vm√R2+ω2L2cos(ωt−φ)+ICOe−tR/L
Now in an inductive circuit I=0 at t=0
because a current cannot change suddently.
Thus ICO=−Vm√R2=ω2L2cosφ
and so I=Vm√R2+ω2L2[cos(ωt−φ)−cosφe−tR/L]
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA capacitor with capacitance C and a coil with active resistance R and inductance L are connected in parallel to a source of sinusoidal voltage of frequency ω. Find the phase difference between the current fed to the circuit and the source voltage.
View Solution
Knowledge Check
A coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
AERBELC√(ER2+L2)D√(ELR2+L2)A coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
AV2/RBV2R(R2+ω2L2)CV2√R2+ω2L2Dzero
In the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
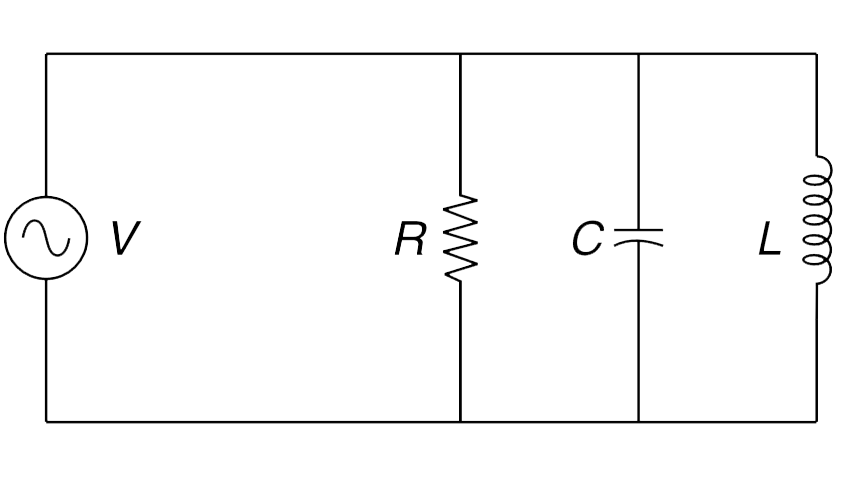
View SolutionA series circuit consisting of a capacitor XC=80Ω and a coil with active resistance R=300Ω and inductance XL=40ω is connected to a source of alternating voltage with amplitude V0=200V Find
(a) the current amplitude in the circuit
(b) the phase difference between the current and voltage
(c) the amplitudes of voltage across the capacitor and the coli .
View SolutionA capacitor with capacitance C whose interelectrode space is filled up with poorly conducting medium with active resistance R is connected to a source of alternating voltage V=Vmcosωt. Find the time dependence of the steady − state current flowing in lead wires. The resistance of the wires is to be neglected.
View SolutionA capacitor with capacitance C=1.0μF and a coil with active resitance R=0.10Ω and inductance L=1.0mH are connected in parallel to a source of sinusoidal voltage V=31V. Find :
(a) the frequency ω at which the resonance sets in ,
(b) the effective value of the fed current in resonance , as well as the corresponding currents flowing through the coil and through the capacitor.
View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View Solution
