A completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
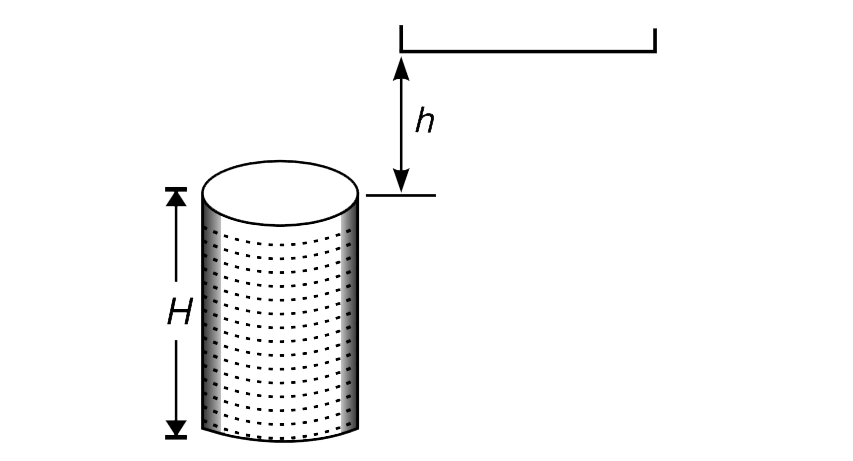
The correct Answer is:p=Mgt0(h+Htt0)
Step by step video, text & image solution for A completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t_0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A tank containing water has an orifice 2 m below the surface of water. If there is no wastage of energy. Find the speed of discharge.
View SolutionA rectangular water tank of base 11m×6m contains water up to a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 1.75 m, find the height of the water level in the tank.
View Solution
Knowledge Check
A cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
A√2hgr2r'2B√2Hgr2r'2C√hHDnone of theseA cylindrical tank contains water up to a height H. If the tank is accelerated upwards with acceleration a, the pressure at the A is p1. If the tank is accelerated downwards with acceleration a the pressure at A is p2. Then
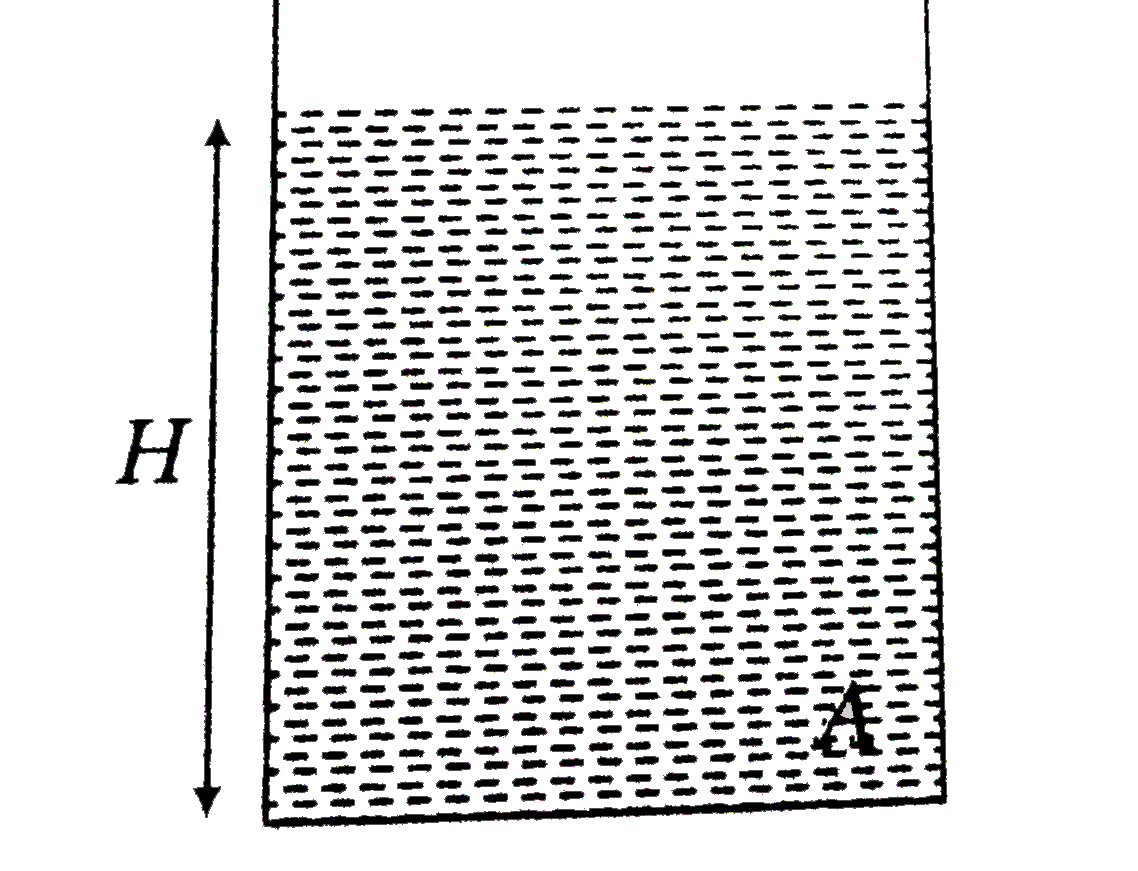 Ap1<p2Bp1=p2Cp1>p2DData insufficient
Ap1<p2Bp1=p2Cp1>p2DData insufficientThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
AHBH2C3H2D√3H2
A rectangular water tank of base 11m×6m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
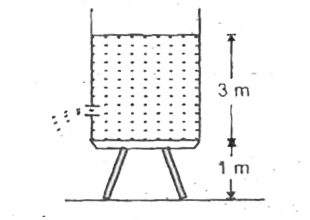
View SolutionThe level of water in a huge tank is 20 m. Nearly at the bottom of the tank, there is a hole of 2 cm? cross section. The rate with which the water will leak through the hole is n×10−3cm. Find the value of n.
View SolutionA cylindrical tank has a hole of 1 cm in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm/sec . then the maximum height up to which water can rise in the tank is
View SolutionThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View Solution
