A conducting circular loop of face are is placed perpendicular to a magnetic field which varies as 10 Omega, find the thermal energy developed in the loop in this period.Solution in Gujrati
The face area of the loop is Phi =B_0 A sin omega tverepsilon =-(dPhi)/(dt) =- B_0 Aomega cos omega t
the current is i= (varepsilon)/(R)=-(B_0 A omega)(R) cos omega t =- i_0 cos omega t
The current changes sinusoidally with the time period Q=int_0^T idt=-i_0 int_0^T cos omega t dt
(b)The thermal energy produced in 40 ms is =(i_0^2 RT)/(2) =(B_0^2 A^2 omega^2)/(2R^2) R((2pi)/(omega)) = (piB_0^2A^2 omega)/(R) =(pi X(0
20T)^2 X(2
5 X10^(-3)m^2)2 X(50pi s^(-1))/(10 Omega) =1
25X10^(-5) J
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer13videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 112videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
A metallic loop is placed in a nonuiform steady magnetic field. Will an emf be induced in the loop?
12:09View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
02:13View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
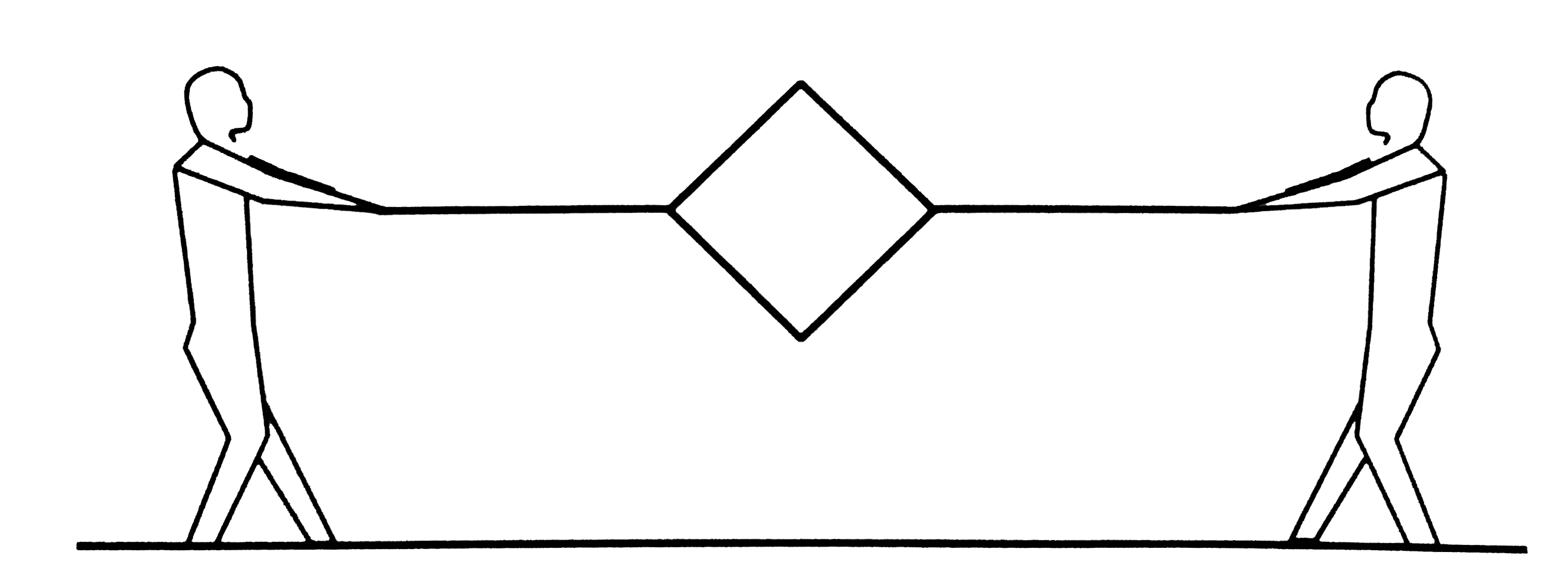 06:28View Solution
06:28View SolutionFind the dimensional formula of ε0 .
02:34View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
02:23View SolutionA conducting circular loop of face are 2.5X10−3m2 is placed perpendicular to a magnetic field which varies as B=(0.20T)sin[(50πs−1)t].(a)F∈dthechar≥jflow∈gthroughanycross−sectiondur∈gthetimet=0→t=40ms.(b)Iftheresistanceofthel∞pis10 Omega, find the thermal energy developed in the loop in this period.
07:39View SolutionA loop of wire enclosing an area S is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field B varies with time according to the expression B=B_0e^(-at) where a is some constant. That is, at t= 0 . The field is B_0 and for t gt 0 , the field decreases exponentially. Find the induced emf in the loop as a function of time.
01:50View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.04:28View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
06:02View SolutionA conducting loop of cross-area A and resistance R is placed perpendicular to a magnetic field B . The loop is withdrawn completely from the field. The change, which flows through any cross-section of the wire in the process
04:32View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B = B_0e^(-t//tau) , where B_0 and tau are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t to oo) is :
03:30View SolutionA circular conducting loop of area 100 cm^(2) and resistance 3 Omega is placed in a magnetic field with its plane perpendicular to the field. If the field is spatially uniform but varies with time t (in second) as B(t) = 1.5 cos omega t tesla, the peak value of the current in the loop is
02:42View SolutionA conducing circular loop of area 2.5xx10^(-3)m^(2) and resistance 10Omega is placed perpendicular to a uniform time varying magnetic field B(t)=0.6 sin(50pit)T . What is the net charge (in mC) flowing through the loop during t = 0 and t = 10 ms ?
05:35View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B = gamma t is applied perpendicular to plane of the loop where gamma is constant and t is time. The induced current flowing through loop is
06:21View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
03:46View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
09:27View Solution

