A conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
power generated in the coil at any time t is constant
flow of charge passed through any section of coil is constant
total charge passed through any section between time .
All of the above
The correct Answer is:D
To solve the problem step by step, we will analyze the given information and apply relevant physics concepts.
Step 1: Understand the Given Information
We have a conducting circular loop of radius a and resistance R. A vertical time-varying magnetic field B=2t is switched on at time t=0.
Step 2: Calculate the Magnetic Flux
The magnetic flux Φ linked with the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
Where:
- B is the magnetic field,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the area.
Since the magnetic field is vertical and the area vector of the loop is also vertical, θ=0 degrees, and cos(0)=1.
The area A of the circular loop is:
A=πa2
Thus, the magnetic flux becomes:
Φ=B⋅A=(2t)⋅(πa2)=2πa2t
Step 3: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) E in the loop is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(2πa2t)=−2πa2
Since we are interested in the magnitude, we have:
E=2πa2
Step 4: Calculate the Current
Using Ohm's law, the current I flowing through the loop can be calculated as:
I=ER=2πa2R
Step 5: Calculate the Power Generated
The power P generated in the loop can be calculated using the formula:
P=I2R
Substituting the expression for current:
P=(2πa2R)2R=4π2a4R
This shows that the power generated is constant since a and R are constants.
Step 6: Calculate the Total Charge Passed
The total charge Q that passes through any section of the coil from t=0 to t=2 can be calculated as:
Q=∫20Idt
Substituting the expression for current:
Q=∫202πa2Rdt=2πa2R∫20dt=2πa2R⋅(2−0)=4πa2R
Conclusion
From the calculations:
1. The power generated in the coil is constant.
2. The flow of charge through any section of the coil is constant.
3. The total charge passed through any section between t=0 to t=2 is 4πa2R.
Thus, all options are correct, and the answer is:
D: All of the above.
We have a conducting circular loop of radius a and resistance R. A vertical time-varying magnetic field B=2t is switched on at time t=0.
The magnetic flux Φ linked with the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
Where:
- B is the magnetic field,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the area.
A=πa2
Thus, the magnetic flux becomes:
Φ=B⋅A=(2t)⋅(πa2)=2πa2t
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) E in the loop is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(2πa2t)=−2πa2
Since we are interested in the magnitude, we have:
E=2πa2
Using Ohm's law, the current I flowing through the loop can be calculated as:
I=ER=2πa2R
The power P generated in the loop can be calculated using the formula:
P=I2R
Substituting the expression for current:
P=(2πa2R)2R=4π2a4R
This shows that the power generated is constant since a and R are constants.
The total charge Q that passes through any section of the coil from t=0 to t=2 can be calculated as:
Q=∫20Idt
Substituting the expression for current:
Q=∫202πa2Rdt=2πa2R∫20dt=2πa2R⋅(2−0)=4πa2R
From the calculations:
1. The power generated in the coil is constant.
2. The flow of charge through any section of the coil is constant.
3. The total charge passed through any section between t=0 to t=2 is 4πa2R.
D: All of the above.
Similar Questions
A non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA uniform conducting ring of mass m=2kg, radius r=2m and resistance 8Ω is kept on smooth, horizontal surface. A time varying magnetic field →B=(ˆi+t2ˆj) Tesla is present in the region, where t is time in second and take vertical as y-axis. (Take π2=10). Then
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
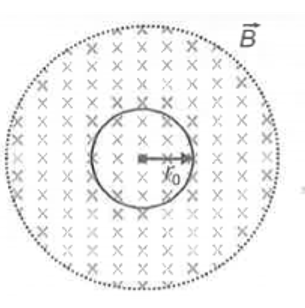
View SolutionA circular conducting coil of radius r0, having resistance R is placed in a time varying transverse uniform magnetic field B=4t2 as shown in the figure. The current in the coil at time t = 2 s is (consider all quantities are in Si units)
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.

View SolutionAn arc of a circular loop of radius R is kept in the horizontal plane and a constant magnetic field B is applied in the vertical direction as shown in the figure . If the arc carries current I then find the force on the arc

View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
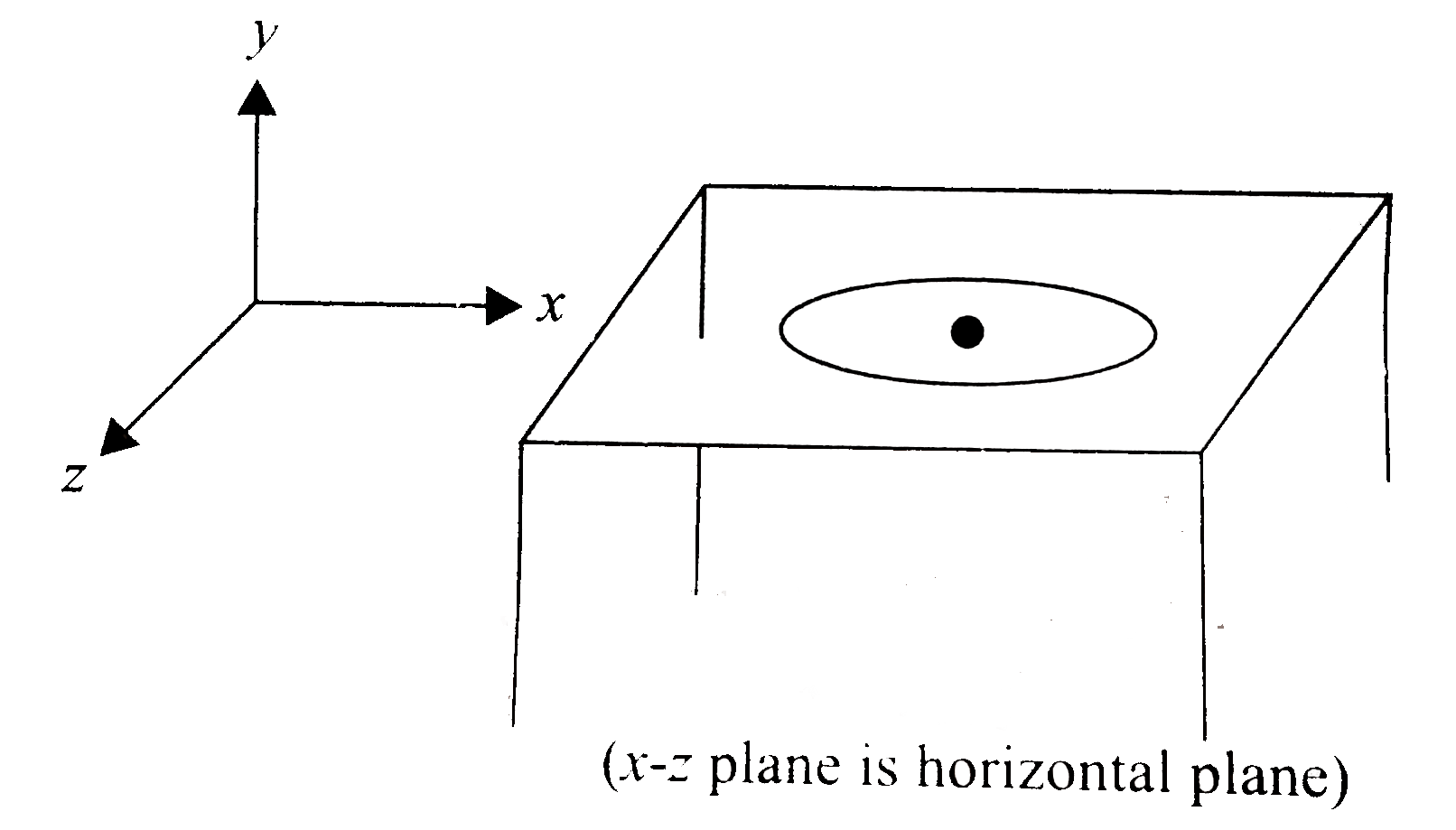
Net Induced EMF (in Volt) on conducting ring as function of time is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
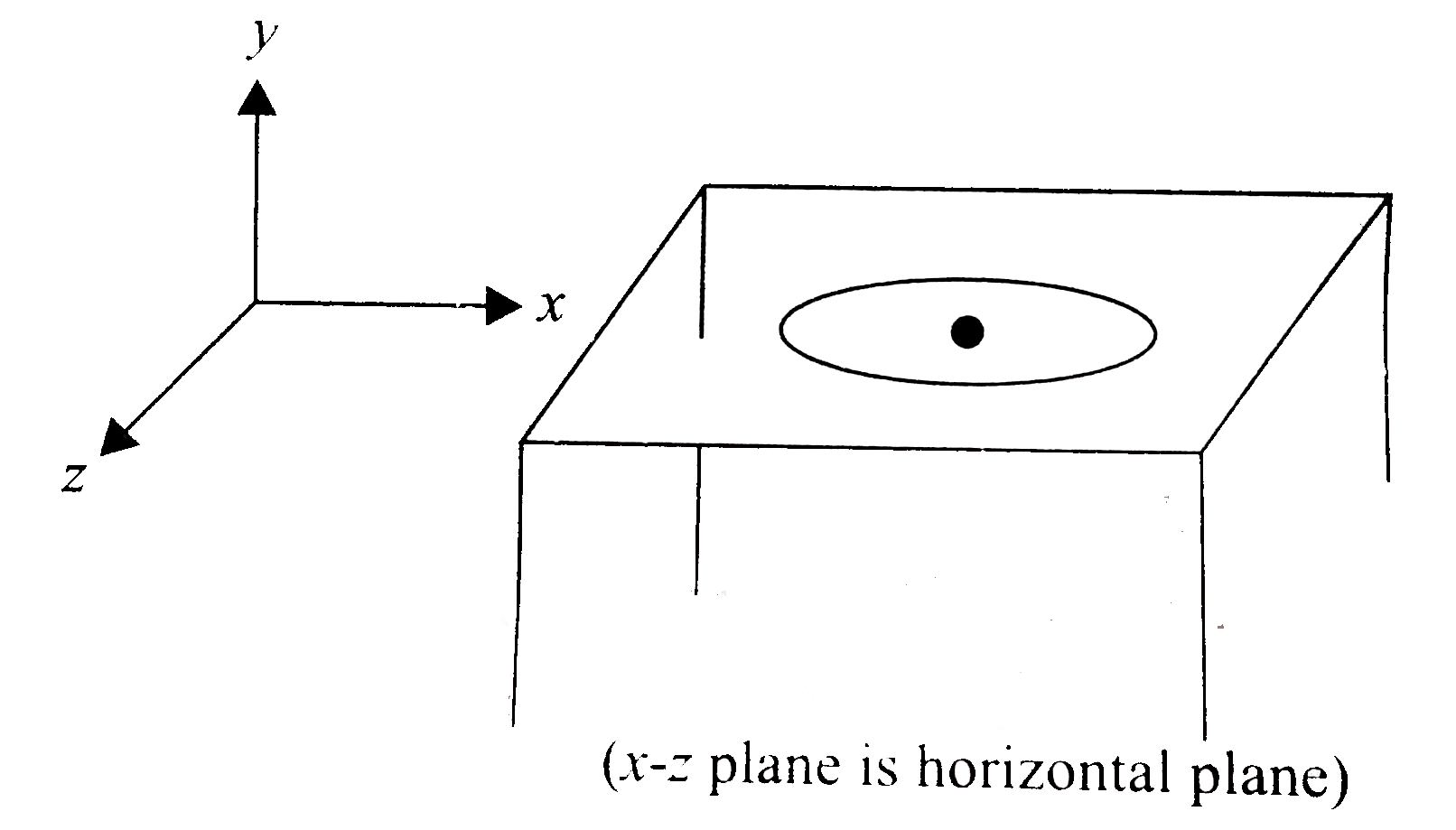
Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling is
View Solution
