A conducting rod rotates with a constant angular velocity 'ω' about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :-
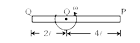
Bl2ω2
0
(Bl2ω8)
2Bl2ω
The correct Answer is:B
Length of the rod between the axis of rotation and one end of the rod =l/2
Area swept out in one rotation =π(l2)2=(πl24)
Angular velocity =ωrads−1
Frequency of revolution =ω2π
Area swept out per second =πl24(ω2π)=l2ω8
Magnetic induction = B
Rate of change of magnetic flux =(Bl2ω8)
Magnitude of induced emf =Bl2ω8
Magnitude of induced emf between the axis and the other and is also (Bl2ω8). These two emfs are in opposite directions. Hence , the potential difference between the two ends of the rod is zero.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (LENZ.S LAW)
1 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (SELF AND MUTUAL INDUCTANCE)
19 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (MAGNETIC FLUX)
1 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
- ELECTROMAGNETIC WAVESBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - AIPMT/NEET(MCQs)
15 Videos
Similar Questions
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View Solution(a) A metal rod of length L rotates about an end with a uniform angular velocity ω . A uniform magnetic field B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they move in circular paths.
(b) A rod of length L rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. Find the potential difference (i) between the centre of rod and one end and (ii) between the two ends of the rod.
View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ωA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
AzeroB12ωBI2CωBI2D2ωBI2A rod of length l is rotated with angular speed ω about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is
ABlω22BBl(ω2)CBlω28DZero
A metallic rod of length lis hinged at one end and the other end is rotated with a constant angular speed ω about an axis passing through the hinge. A constant and uniform magnetic field B, parallel to the axis of rotation exists everywhere. The induced emf between the two ends of rod is 12Blω2.
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View Solutionif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View SolutionA conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View Solution
