A conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
rx
rx2
2rx
4rx
The correct Answer is:B
Let →E be the electric field intensity at a point on the circumference of the ring . Then , the emf induced ε=∮→E.→dl where →dl is a length element of the ring . Since ∣∣→E∣∣ is constant and →E∣∣→dl
∴ε=E(2πr) .....(i)
Also , the induced emf is
ε=dϕdt=πr2dBdt=πr2x ......(ii)
Equating (i) and (ii) , we get E=rx2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (LENZ.S LAW)
1 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (SELF AND MUTUAL INDUCTANCE)
19 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (MAGNETIC FLUX)
1 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
- ELECTROMAGNETIC WAVESBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - AIPMT/NEET(MCQs)
15 Videos
Similar Questions
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View Solution
Knowledge Check
Electric field intensity at a point varies as r−3 for
AA point chargeBAn electric dipoleCA plane infinite sheet of chargeDA line charge of infinite lengthA nonconducting of radius r has charge Q. A magnetic field perpendicular to the plane of ring changes at the rate dBdt. The torque experienced by the ring is
AzeroBQr2dBdtC12Qr2dBdtDπr2QdBdtA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
AIt is rotated about it axisBit is translatedCit is rotated about a diameterDit is deformed
the uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
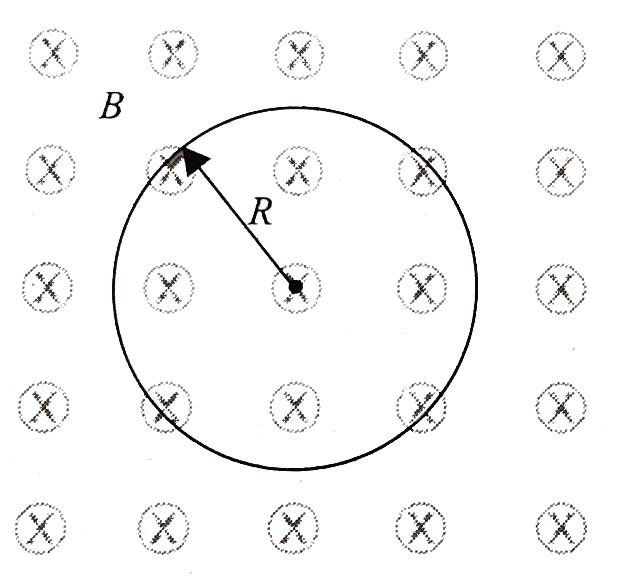
View SolutionA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionA non-conducting ring of radius r has charge per unit length λ. A magnetic field perpendicular to plane of the ring changes at rate Db/dt. Torque experienced by the ring is
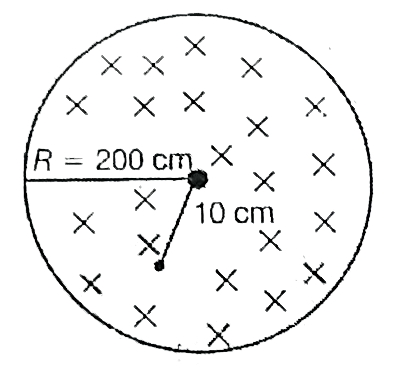
View Solution
