A conducting sphere of radius r has a charge . Then .
the charge is uniformly distributed over its surface, if there is no external electric field
the distribution of charge over its surface will be nonuniform if an external electric field exists in the space.
the potential at every point of the sphere must be the same
the electric field strength inside the sphere will be equal to zero only when no external electric field exists.
The correct Answer is:A, B, C
a.,b.,c.
If there is no external electric field, then the charge given to a conducting sphere gets uniformly distributed over its surface. Therefore, option (a) is correct. If an external electric field exists, then the charge gets distributed over the surface of the sphere in such a way that the electric field inside the sphere can become equal to zero. Hence. distribution of the charge on the surface of sphere will be non-uniform. Therefore, option (b) is correct. Obviously, option (d) is wrong.
Since electric field inside the conducting sphere is equal to zero. potential difference between two points in the sphere is equal to zero. It means , the potential is same at every point of the sphere. Therefore, option (c) is correct.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A conducting sphere of radius R carries a charge Q. It is enclosed by another concentric spherical shell of radius 2R. Charge from the inner sphere is transferred in infinitesimally small installments to the outer sphere. Calculate the work done in transferring the entire charge from the inner sphere to the outer one.
View SolutionA conducting sphere of radius α has charge Q .on it.It is enclosed by a neutral conducting concentric spherical shell having inner radius 2α and outer radius 3α.Find electrostatic energy of system
View Solution
Knowledge Check
A hollow conducting sphere of radius R has a charge (+Q) on its surface. What is the electric potential within the
sphere at a distance r=R3 from its centre ?AZeroB14πε0QrC14πε0QRD14πε0Qr2A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
AZero and Q4πε0R2BQ4πε0R2 and zeroCQ4πε0R and Q4πε0R2DBoth are zeroTwo concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
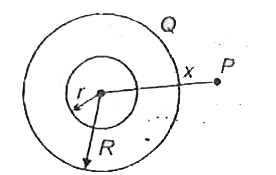 AQrRB−QRrC−QD−2QRr
AQrRB−QRrC−QD−2QRr
A conducting sphere of radius r is charged to a potential V .The outward pull per unit area of its surface is given by...
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is

View Solution
