Question

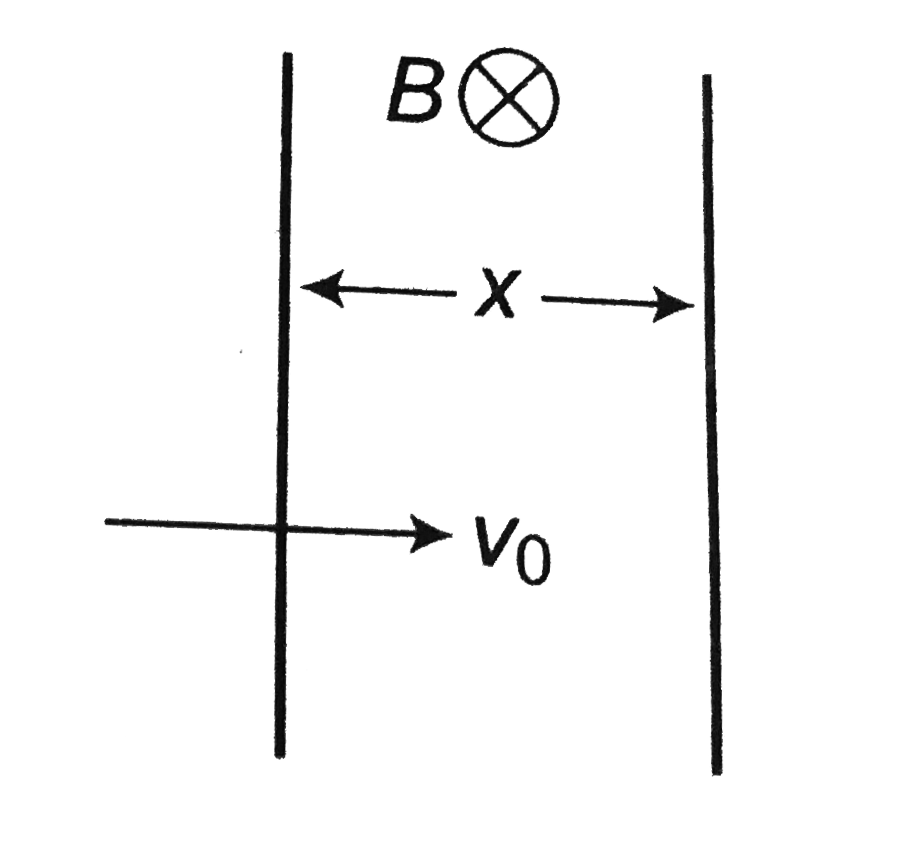
A charged particle enters a uniform magnetic field with velocity $v_0=4m/s$ perpendicular to it, the length of magnetic field is $x=\left(\frac{\sqrt{3}}{2}\right)R$, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.

Answer

4

Explanation

To solve the problem step by step, we need to analyze the motion of a charged particle entering a uniform magnetic field and determine its velocity when it exits the field.

Step 1: Understand the motion of the particle
The charged particle enters a uniform magnetic field with an initial velocity \( v_0 = 4 \, \text{m/s} \) perpendicular to the field. The particle will follow a circular path due to the magnetic force acting on it.

Step 2: Determine the radius of the circular path
The radius \( R \) of the circular path is related to the length of the magnetic field \( x \) given by:
\( x = \frac{\sqrt{3}}{2} R \)
This means that the particle will travel a circular arc of length \( x \) within the magnetic field.

Step 3: Calculate the angle subtended by the arc
The angle \( \theta \) subtended by the arc can be calculated using the formula for the length of an arc:
\( x = R \theta \)
Substituting the expression for \( x \):
\( \frac{\sqrt{3}}{2} R = R \theta \implies \theta = \frac{\sqrt{3}}{2} \)
However, we need to express this in radians for further calculations. The angle in radians corresponding to \( \frac{\sqrt{3}}{2} \) is not straightforward, so we will use the relationship between the arc length and the radius to find the angle directly.

Step 4: Calculate the angular displacement
The total angle \( \theta \) in radians can be calculated as:
\( \theta = \frac{x}{R} = \frac{\frac{\sqrt{3}}{2} R}{R} = \frac{\sqrt{3}}{2} \)
This angle corresponds to \( 60^\circ \) or \( \frac{\pi}{3} \) radians.

Step 5: Determine the components of the velocity
When the particle exits the magnetic field, it will have two components of velocity due to the circular motion:
- The radial component \( v_r = v_0 \cos(60^\circ) = v_0 \cdot \frac{1}{2} = 2 \, \text{m/s} \)
- The tangential component \( v_t = v_0 \sin(60^\circ) = v_0 \cdot \frac{\sqrt{3}}{2} = 4 \cdot \frac{\sqrt{3}}{2} = 2\sqrt{3} \, \text{m/s} \)

Step 6: Calculate the resultant velocity
The resultant velocity \( v_f \) when the particle exits the magnetic field can be found using the Pythagorean theorem:
\( v_f = \sqrt{(v_r)^2 + (v_t)^2} = \sqrt{(2)^2 + (2\sqrt{3})^2} = \sqrt{4 + 12} = \sqrt{16} = 4 \, \text{m/s} \)

Conclusion
The magnitude of the velocity of the particle when it comes out of the field is \( 4 \, \text{m/s} \).