A conducting wire XY of mass m and neglibile resistance slides smoothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field

(i) Write down equation for the acceleration of the wire XY.
(ii) If is independent of time, obtain v(t), assuming v (0) =.
(iii) For (ii), show that the decrease in kinetic energy of XY equals the heat lost in.Solution in Gujrati
Suppose two parallel wire are at y = 0 and y = l
Suppose at t = 0 time wire xy is at x = 0 and at t = t time it is at x = x place.
(i) Magnetic flux linked with closed loop,
=[B(t)](lx)
Induced emf,
....(1)
(Motional emf) (emf due to variation in magnetic field)
Magnetic force on wire ,
F=IlB(t)
Acceleration of wire,
...(2)
(ii) If magnetic field does not change with time
Taking integration and at t=0, v=
...(3)
(iii) Change in kinetic energy of wire,
...(4)
Power dissipated in the terms of heat,
...(5)
If B is constant then from equation (1),
...(6)
From equation (5) and (6) it is clear that change in kinetic energy is equal to produced heat energy.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (From DARPAN Based on Textbook )
121 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section C Ncert Exemplar Solution (Short Answer )
5 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
14 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
Similar Questions
When a metallic rod falls freely, keeping its length horizontal and parallel to north-south direction, emf induced across it is ______
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionA magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionFigure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Omega//m . Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0 The current in the loop at t=0 due to induced emf is
View SolutionA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C . The conductor is relased from rest when it is very close to AC i.e., y = 0 . A uniform magnetic field B_(0) perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g . Based on above information answer the following questions: Current in the circuit is
View SolutionA conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field vecB=-Bhatk is existing in the region. The net magnetic force experenced by the conducting wire MN is
View SolutionTwo parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are lamda no other wire has resistance. Then :
View SolutionA conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t)hatk
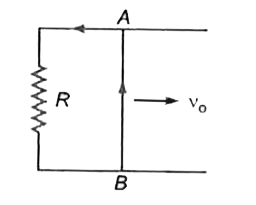
View SolutionTwo long parallel metallic wires with a resistance 'R' from a horizontal plane . A conducting rod AB is on the wires shown in figure . The space has magnetic field pointing vertically downwards. The rod is given an initial velocity 'v_(0)' . There is no friction in the wire and the rod . After a time 't' the velocity v of the rod will be such that :-
View SolutionA conducting wire ab of length l resistance r and mass m starts sliding down at t=0 on a smooth, vertical thick pair of connected rails as shown. The terminal speed of the wire is

View Solutionदो लम्बी समान्तर धातु की तारें एक प्रतिरोध R के साथ क्षैतिज तल बनाती है। एक चालक छड़ AB चित्रानुसार तार पर रखी है। दिक्स्थान का चुम्बकीय क्षेत्र ऊर्ध्वाधर ऊपर की ओर है छड़ को प्रारम्भिक वेग v0 दिया गया है। निकाय घर्षणहीन है तथा छड़ में कोई प्रतिरोध नहीं है। t समय पश्चात् छड़ का वेग v इस प्रकार होगा कि
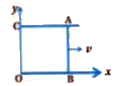
View SolutionA magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
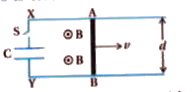
View SolutionFind the current in the sliding rod AB (resistance = R) for the arrangement shown in figure. →B is constant and is out of the paper. Parallel wires have no resistance, v is constant. Switch S is closed at time t = 0.
View Solution
