A constant electric field of intensity 36N/C exists along the z-axis. If P and Q be two points whose coordinates are (10 cm, 0, -20 cm) and (0, -10 cm, 30 cm) respectively, then find the potential difference VP−VQ.
The correct Answer is:18V
To find the potential difference VP−VQ between the points P and Q in a constant electric field, we can follow these steps:
Step 1: Identify the electric field and its direction
The electric field intensity is given as E=36N/C along the z-axis. This means that the electric field vector can be represented as:
→E=36^kN/C
Step 2: Identify the coordinates of points P and Q
The coordinates of the points are:
- Point P: (10cm,0,−20cm) or (0.1m,0,−0.2m)
- Point Q: (0,−10cm,30cm) or (0,−0.1m,0.3m)
Step 3: Calculate the potential difference using the formula
The potential difference VP−VQ in an electric field can be calculated using the formula:
VP−VQ=−∫PQ→E⋅d→r
Since the electric field is constant and directed along the z-axis, we can simplify the integral.
Step 4: Determine the change in the z-coordinate
The z-coordinates for points P and Q are:
- For P: zP=−20cm=−0.2m
- For Q: zQ=30cm=0.3m
The change in z-coordinate as we move from Q to P is:
zP−zQ=−0.2−0.3=−0.5m
Step 5: Substitute into the potential difference formula
Substituting the values into the potential difference formula gives:
VP−VQ=−∫PQ→E⋅d→r=−E⋅(zP−zQ)
Substituting E=36N/C:
VP−VQ=−36⋅(−0.5)=18V
Final Answer
Thus, the potential difference VP−VQ is:
VP−VQ=18V
The electric field intensity is given as E=36N/C along the z-axis. This means that the electric field vector can be represented as:
→E=36^kN/C
The coordinates of the points are:
- Point P: (10cm,0,−20cm) or (0.1m,0,−0.2m)
- Point Q: (0,−10cm,30cm) or (0,−0.1m,0.3m)
The potential difference VP−VQ in an electric field can be calculated using the formula:
VP−VQ=−∫PQ→E⋅d→r
Since the electric field is constant and directed along the z-axis, we can simplify the integral.
The z-coordinates for points P and Q are:
- For P: zP=−20cm=−0.2m
- For Q: zQ=30cm=0.3m
zP−zQ=−0.2−0.3=−0.5m
Substituting the values into the potential difference formula gives:
VP−VQ=−∫PQ→E⋅d→r=−E⋅(zP−zQ)
Substituting E=36N/C:
VP−VQ=−36⋅(−0.5)=18V
Thus, the potential difference VP−VQ is:
VP−VQ=18V
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)
23 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
11 Videos
Similar Questions
Find the volume of a box if its length, breadth and height are 20 cm, 10 cm and 30 cm respectively.
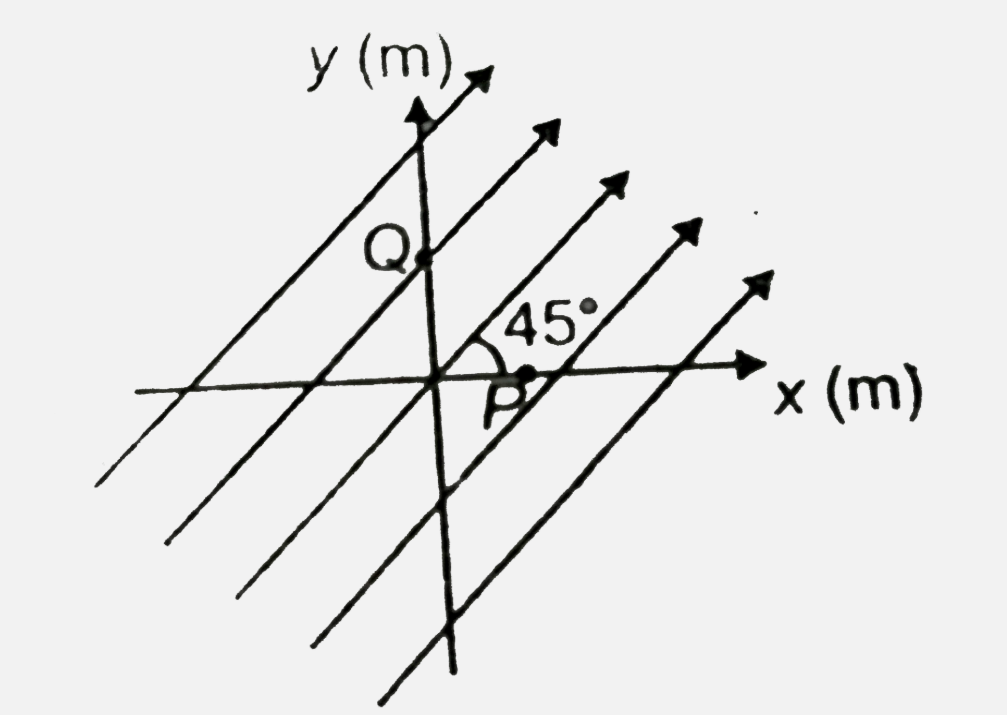
View SolutionA uniform electric field of 200 V / m is directed at 45∘ with x -axis as shown in figure. The co-ordinates of point P and point Q are (1,0) and ( 0,2) . Find the potential difference , VP−VQ ( in volts) .
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionIn a uniform electric field, the potential is 10V at the origin of coordinates , and 8V at each of the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). The potential at the point (1, 1,1 ) will be .
View SolutionA uniform electric field E0 exists in a region at angle 45∘ with the x - axis. There are two point A(a,0)andB(0,b) having potential VAandVB, respectively, then
 .
.
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
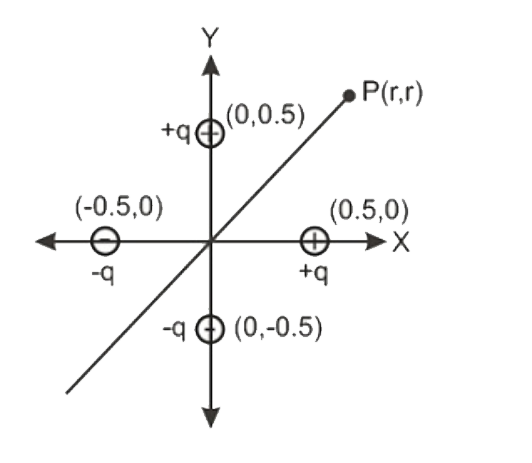
The electric field due to these charges at a point P(r,r), where r>>0.5, will be
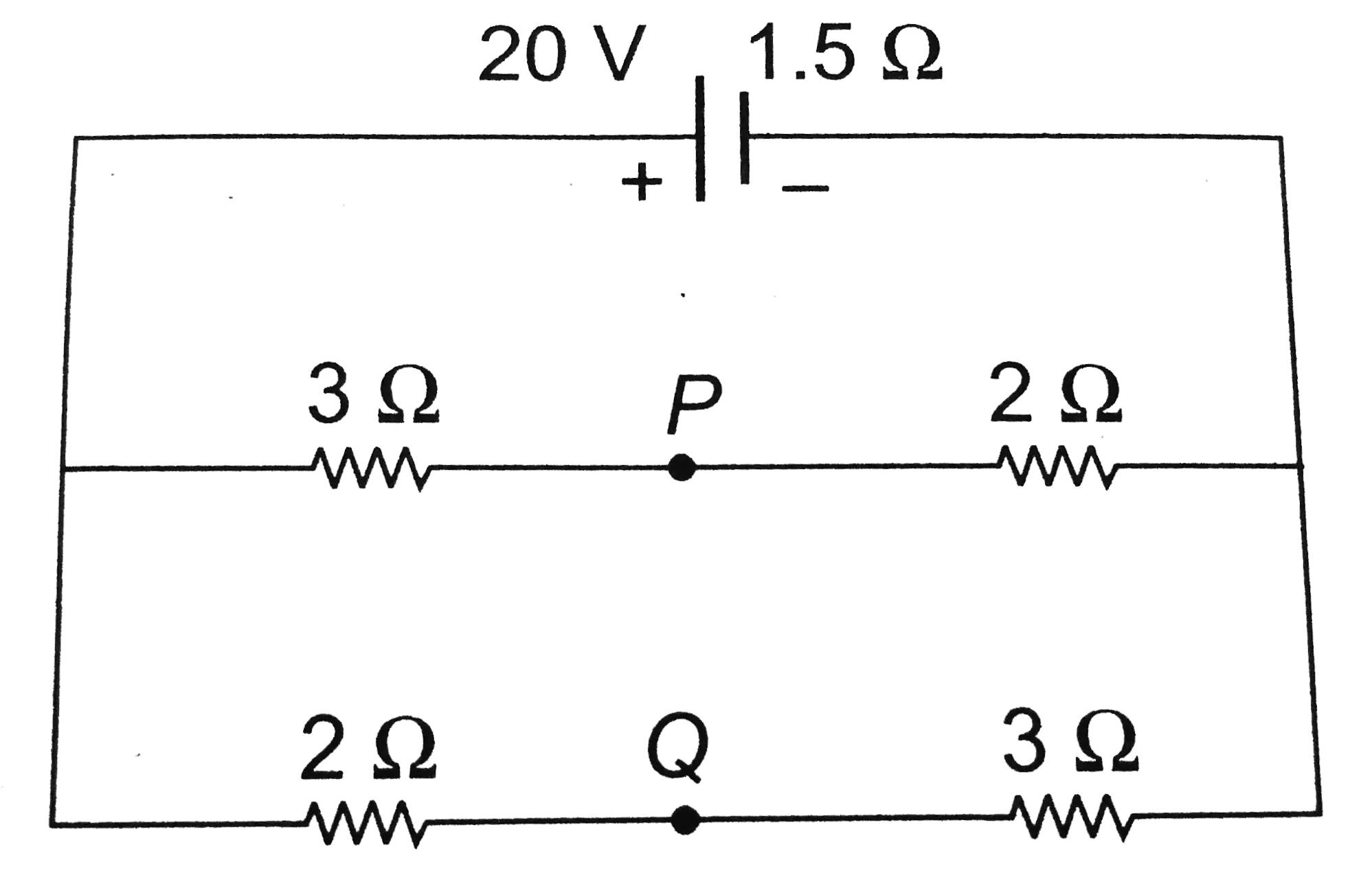
View SolutionIf in the circuit shown below, the internal resistance of the battery is 1.5Ω and VP and VQ are the potential at P and Q respectively, what is the potential difference between the point P and Q?
View SolutionA nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
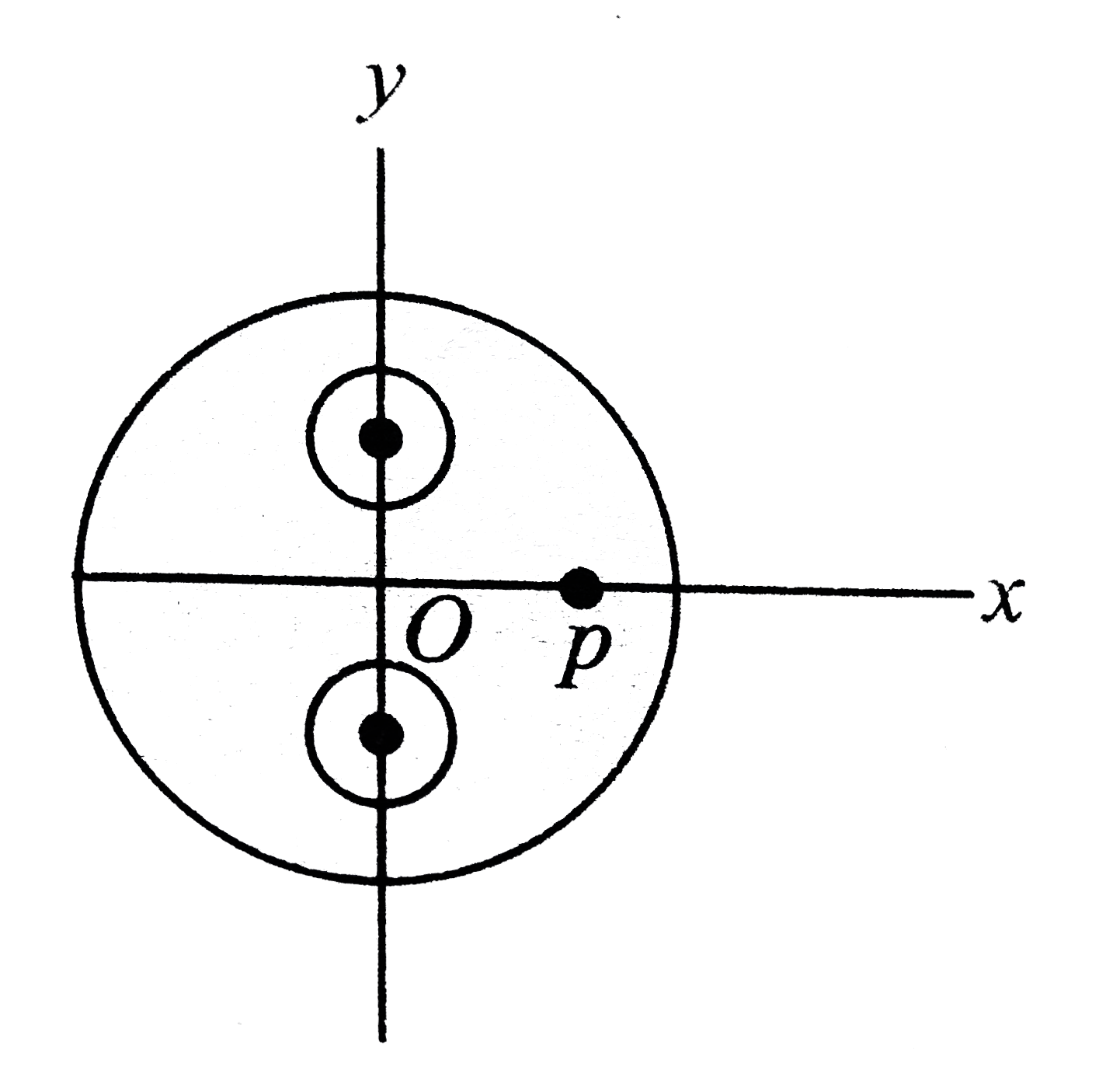 .
.
View SolutionA uniform electric field of magnitude 250V/m is directed in the positive x-direction. A+12μC charge moves from the origin to the point (x,y)=(20.0cm,5.0cm).
(a) What was the change in the potential energy of this charge?
(b) Through what potential difference did the charge move?
View Solution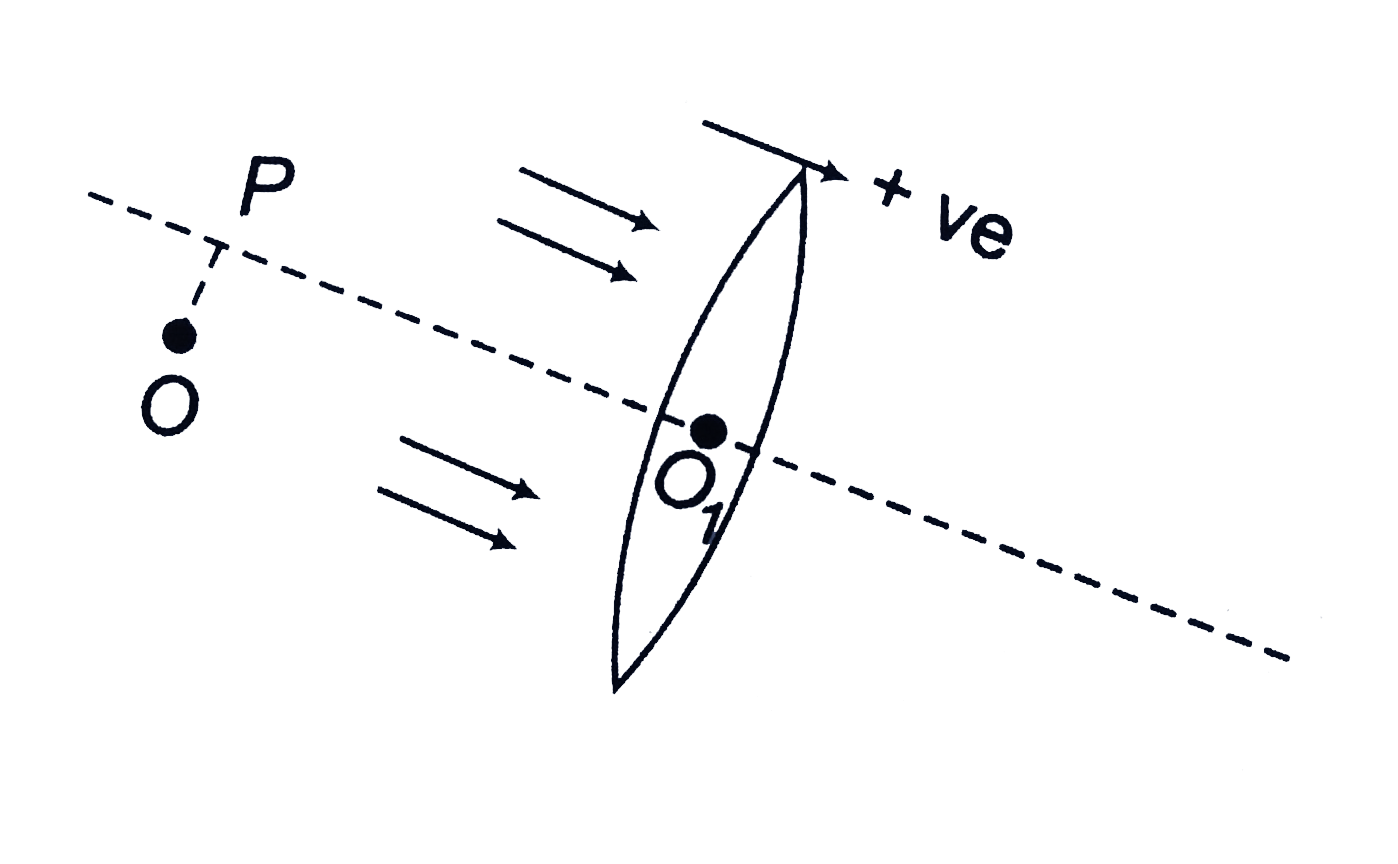
O1P is the principal axis and O is the point object. Given,
O1P=30cm,f=20cm and OP=2mm. Find the image distance and its position.
View Solution
