Question

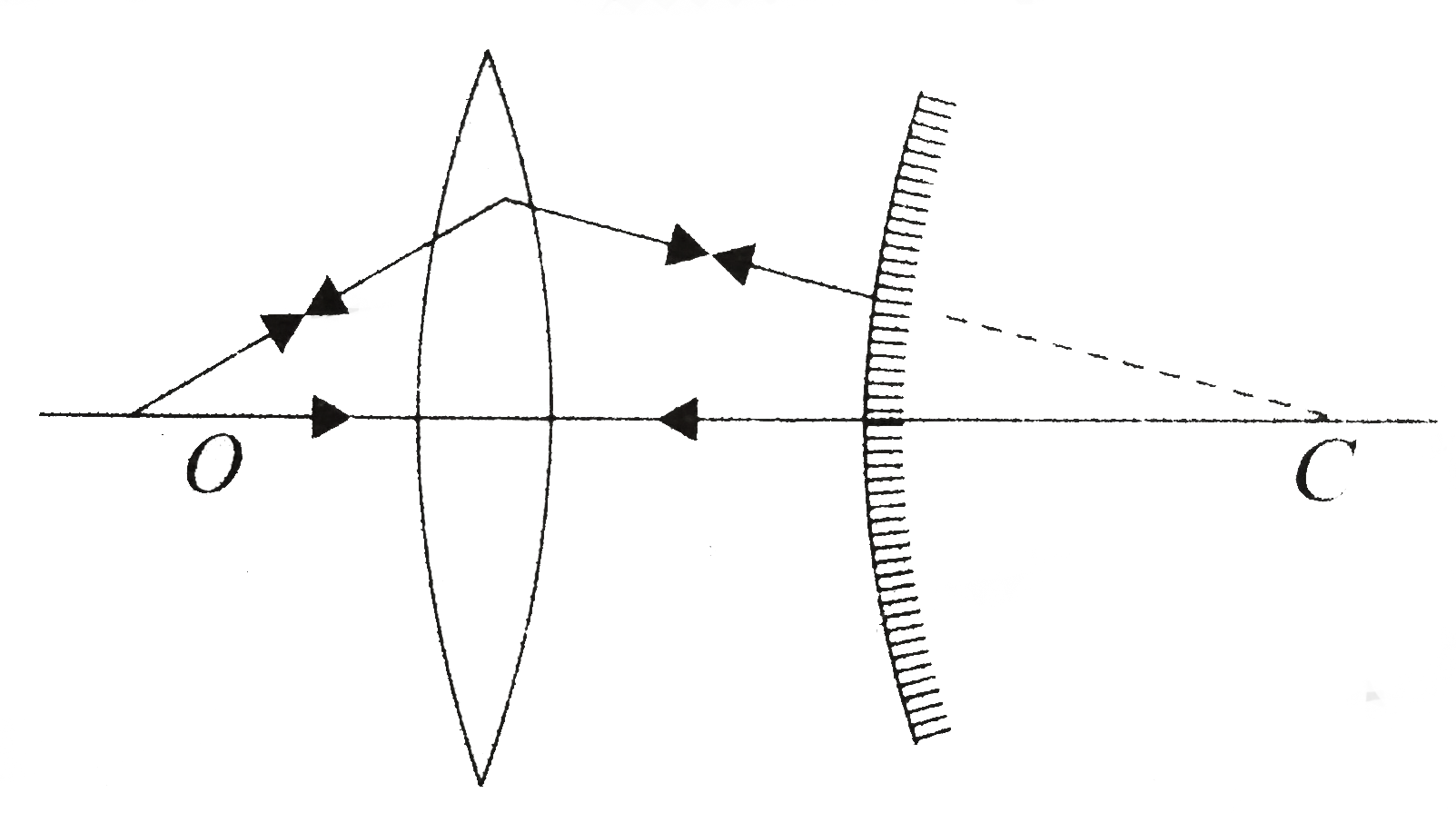
A convex lens and a convex mirror of radius of curvature $20cm$ are placed co-axially with the convex mirror placed at a distance of $30cm$ from the lens. For a point object at a distance of $25cm$ from the lens, the final image due to this combination coincides with the object itself. What is the focal length of convex lens ?

Explanation

To find the focal length of the convex lens in the given setup, we can follow these steps:

Step 1: Understand the Setup
We have a convex lens and a convex mirror placed coaxially. The radius of curvature (R) of the convex mirror is given as 20 cm. The distance between the lens and the mirror is 30 cm, and there is a point object located 25 cm from the lens.

Step 2: Determine the Focal Length of the Convex Mirror
The focal length (f) of a mirror is related to its radius of curvature (R) by the formula:
\( f = \frac{R}{2} \)
For the convex mirror:
\( f_{mirror} = \frac{20 \, \text{cm}}{2} = 10 \, \text{cm} \)
Since it is a convex mirror, the focal length is positive:
\( f_{mirror} = +10 \, \text{cm} \)

Step 3: Find the Image Distance from the Mirror
The object is located 25 cm from the lens, and the distance from the lens to the mirror is 30 cm. Therefore, the distance of the object from the mirror (u_mirror) can be calculated as:
\( u_{mirror} = 30 \, \text{cm} - 25 \, \text{cm} = 5 \, \text{cm} \)
Since the object is in front of the mirror, we consider this distance as negative:
\( u_{mirror} = -5 \, \text{cm} \)

Step 4: Use the Mirror Formula to Find the Image Distance
The mirror formula is given by:
\( \frac{1}{f} = \frac{1}{v} + \frac{1}{u} \)
Here, \( f = +10 \, \text{cm} \) and \( u = -5 \, \text{cm} \). Rearranging the formula gives:
\( \frac{1}{v} = \frac{1}{f} - \frac{1}{u} \)
Substituting the values:
\( \frac{1}{v} = \frac{1}{10} - \frac{1}{-5} \)
\( \frac{1}{v} = \frac{1}{10} + \frac{1}{5} \)
Converting \( \frac{1}{5} \) to a common denominator:
\( \frac{1}{5} = \frac{2}{10} \)
So,
\( \frac{1}{v} = \frac{1}{10} + \frac{2}{10} = \frac{3}{10} \)
Thus,
\( v = \frac{10}{3} \, \text{cm} \)

Step 5: Find the Image Distance from the Lens
The image formed by the mirror acts as a virtual object for the lens. The distance from the lens to this image (v_lens) is:
\( v_{lens} = 30 \, \text{cm} + \frac{10}{3} \, \text{cm} = \frac{90}{3} + \frac{10}{3} = \frac{100}{3} \, \text{cm} \)

Step 6: Use the Lens Formula to Find the Focal Length
The lens formula is:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
Where:
- \( v = \frac{100}{3} \, \text{cm} \) (positive since the image is on the opposite side of the lens)
- \( u = -25 \, \text{cm} \)

Substituting these values into the lens formula:
\( \frac{1}{f} = \frac{3}{100} - \frac{1}{-25} \)
Converting \( -\frac{1}{25} \) to a common denominator:
\( -\frac{1}{25} = -\frac{4}{100} \)
So,
\( \frac{1}{f} = \frac{3}{100} + \frac{4}{100} = \frac{7}{100} \)
Thus,
\( f = \frac{100}{7} \, \text{cm} \approx 14.29 \, \text{cm} \)

Final Answer
The focal length of the convex lens is approximately \( 14.29 \, \text{cm} \).

---