A convex lens forms an image of an object placed 20cm away from it at a distance of 20cm on the other side of the lens. If the object is moves 5cm toward the lens, the image will be
5cm toward the lens
5cm away from the lens
10cm toward the lens
10cm away from the lens
The correct Answer is:d.
To solve the problem, we will use the lens formula and follow these steps:
Step 1: Understand the given information
We have a convex lens with the following details:
- The initial object distance (u) = -20 cm (the negative sign indicates that the object is on the same side as the incoming light).
- The image distance (v) = +20 cm (the positive sign indicates that the image is formed on the opposite side of the lens).
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
Substituting the known values:
1f=120−1−20
This simplifies to:
1f=120+120=220=110
Thus, the focal length (f) of the lens is:
f=10 cm
Step 3: Update the object distance
The object is moved 5 cm closer to the lens. Therefore, the new object distance (u') is:
u′=−20 cm+5 cm=−15 cm
Step 4: Calculate the new image distance
Now, we will use the lens formula again to find the new image distance (v'):
1f=1v′−1u′
Substituting the values we have:
110=1v′−1−15
This simplifies to:
110=1v′+115
To combine the fractions, we need a common denominator, which is 30:
110=330and115=230
So we have:
330=1v′+230
Rearranging gives:
1v′=330−230=130
Thus, the new image distance (v') is:
v′=30 cm
Step 5: Interpret the result
The new image distance of 30 cm indicates that the image has moved further away from the lens compared to the previous position of 20 cm.
Final Answer
The new image distance is 30 cm, meaning the image has moved 10 cm away from the lens.
---
We have a convex lens with the following details:
- The initial object distance (u) = -20 cm (the negative sign indicates that the object is on the same side as the incoming light).
- The image distance (v) = +20 cm (the positive sign indicates that the image is formed on the opposite side of the lens).
The lens formula is given by:
1f=1v−1u
Substituting the known values:
1f=120−1−20
This simplifies to:
1f=120+120=220=110
Thus, the focal length (f) of the lens is:
f=10 cm
The object is moved 5 cm closer to the lens. Therefore, the new object distance (u') is:
u′=−20 cm+5 cm=−15 cm
Now, we will use the lens formula again to find the new image distance (v'):
1f=1v′−1u′
Substituting the values we have:
110=1v′−1−15
This simplifies to:
110=1v′+115
To combine the fractions, we need a common denominator, which is 30:
110=330and115=230
So we have:
330=1v′+230
Rearranging gives:
1v′=330−230=130
Thus, the new image distance (v') is:
v′=30 cm
The new image distance of 30 cm indicates that the image has moved further away from the lens compared to the previous position of 20 cm.
The new image distance is 30 cm, meaning the image has moved 10 cm away from the lens.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
View SolutionA point object O is placed on the principal axis of a convex lens of focal length f=20cm at a distance of 40 cm to the left of it. The diameter of the lens is 10. An eye is placed 60 cm to right of the lens and a distance h below the principal axis. The maximum value of h to see the image is
View Solution
Knowledge Check
The image of a needle placed 45cm from a lens is formed on a screen placed 90cm on the other side of lens. Find displacement of image if object is moved 5cm away from lens.
A10cm, towards the lensB15cm, away from the lensC15cm, towards the lensD10cm, away from the lensA real image of an object is formed at a distance of 20cm from a lens. On putting another lens in contact with it, the image is shifted 10cm towards the combination, Determine the power of the second lens.
A2DB5DC6DD10 D
A thin converging lens of focal length f = 25 cm forms the image of an object on a screen placed at a distance of 75 cm from the lens. Now the screen in moved closer to the lens by a distance of 25 cm. The distance through which the object has to be shifted so that its image on the screen is sharp again is
View SolutionA convex lens forms a real and inverted image of a needle at a distance of 50cm from it. Where is the needle placed in front of the convex lens if the image is equal to size of the object ? Also, find the power of the lens.
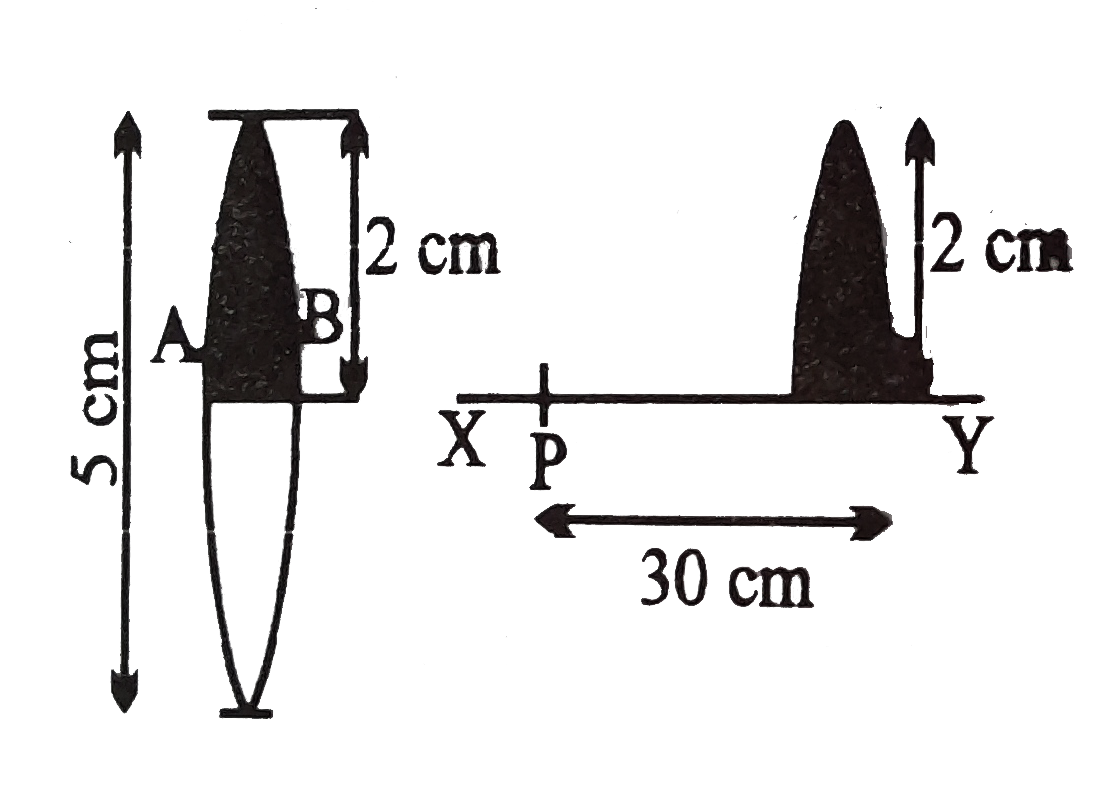
View SolutionA converging lens of focal length 20cmand diameter5cmis cut along the lineAB.The part of the lens shown shaded in the diagram is now used to form an image of a point Pplaced 30cmaway from it on the lineXY.Which id perpendicualr to the plane of the lens.The image ofPwill be formed.
View SolutionA convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
View SolutionThe image of a candle flame formed by a lens is obtained on a screen placed on the other side of the lens. If the image is three times the size of the flame and the distance between lens and image is 80cm, at what distance should the candle be placed from the lens ? What is the nature of the image at a distance of 80cm from the lens ?
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View Solution
