A coolie carries a load of 50 kg on his head and walks on a level road upto 100m. What is the work done by him?
To solve the problem of calculating the work done by the coolie carrying a load of 50 kg while walking on a level road for a distance of 100 meters, we can follow these steps:
1. Identify the Force Acting on the Load:
The coolie is carrying a load of 50 kg. The force acting on this load is its weight, which can be calculated using the formula:
Weight (Force)=m×g
where m=50kg (mass of the load) and g=9.8m/s2 (acceleration due to gravity).
2. Calculate the Weight:
Weight=50kg×9.8m/s2=490N
So, the force exerted by the coolie is 490 N downward.
3. Determine the Displacement:
The coolie walks a distance of 100 meters horizontally.
4. Identify the Angle Between Force and Displacement:
The force (weight) acts vertically downward, while the displacement is horizontal. Therefore, the angle θ between the force and the displacement is:
θ=90∘
5. Use the Work Done Formula:
The work done W is calculated using the formula:
W=F×d×cos(θ)
where F is the force, d is the displacement, and θ is the angle between the force and displacement.
6. Substitute the Values:
W=490N×100m×cos(90∘)
Since cos(90∘)=0:
W=490N×100m×0=0
7. Conclusion:
The work done by the coolie while carrying the load on a level road is:
W=0Joules
The coolie is carrying a load of 50 kg. The force acting on this load is its weight, which can be calculated using the formula:
Weight (Force)=m×g
where m=50kg (mass of the load) and g=9.8m/s2 (acceleration due to gravity).
Weight=50kg×9.8m/s2=490N
So, the force exerted by the coolie is 490 N downward.
The coolie walks a distance of 100 meters horizontally.
The force (weight) acts vertically downward, while the displacement is horizontal. Therefore, the angle θ between the force and the displacement is:
θ=90∘
The work done W is calculated using the formula:
W=F×d×cos(θ)
where F is the force, d is the displacement, and θ is the angle between the force and displacement.
W=490N×100m×cos(90∘)
Since cos(90∘)=0:
W=490N×100m×0=0
The work done by the coolie while carrying the load on a level road is:
W=0Joules
Topper's Solved these Questions
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Continuous Assessment
24 Videos
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Assessment Through paper pen Test
30 Videos
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Multiple choice Questions
9 Videos
- SOUNDBOOK - PRADEEPCHAPTER - SOUNDEXERCISE - Model Test (sec - B)
12 Videos
Similar Questions
Knowledge Check
A man carries a load of 5 kg on his head through a distance of 10 m. the minimum amount of work is done when he
AMove it up an inclined planeBMoves it down an inclined planeCMoves it over a horizontal surfaceDLifts it vertically upwards.A man weighing 100 kg carriesa load of 10kg on his head. He jumps from a tower with the load on his head. What will be the weight of the load as experienced by the man?
AzeroB10kgCslightly more than 10 kgD110 kgA man of mass 65 kg is holding a bucket of mass 15 kg. He walks 50 m on a level road at a constant speed of 3 m/s and then climbs up a hill of height 20 m. What is the work done by the man? Takeg=10ms2.
A2.05kJB3.5kJC12kJD16kJ
A boy carries a 10 kg load from point C to A along the path CA as shown in the figure. What is te work done by the boy against the gravitational pull of the earth ?
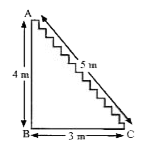
View SolutionConsider the situation - A laborer carrying bricks on his head on a level road from one place to another. Find the work done in the process (a) by gravity, (b) by man (c) by frictional force between man and ground.
View SolutionA boy is moving on a straight road against a frictional force of 5 N. After travelling a distance of 1.5 km, he forgot the correct path at a round about, of radius 100m. However, he moves on the circular path for one and half cycle and then he moves forward upto 2.0 km. Calculate the work done by him.

View SolutionA man weighing 70kg carries a weight of 10kg on the top of a tower 100 m high. Calculate the work done by the man. (g=10m/s2)
View SolutionA man starts walking from a point on the surface of earth (assumed smooth ) and reaches diagonally opposite point . What is the work done by him.
View Solution
