A cube of uniform density and edge a is balanced on a cylindrical surface of radius r. Shown that the criterion for stability of equilibrium of the cube, assuming that fraction is sufficient to prevent slipping, is r>a/2
Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
Similar Questions
A hemispherical cup of radius r with its centre of gravity at C distant c from its centre rests on the top of a spherical surface of radius R as shown in figure 6.15 .Assuming that there is sufficient friction to prevent slipping , establish the criterion of stablility of the cup in the position shown.

View Solution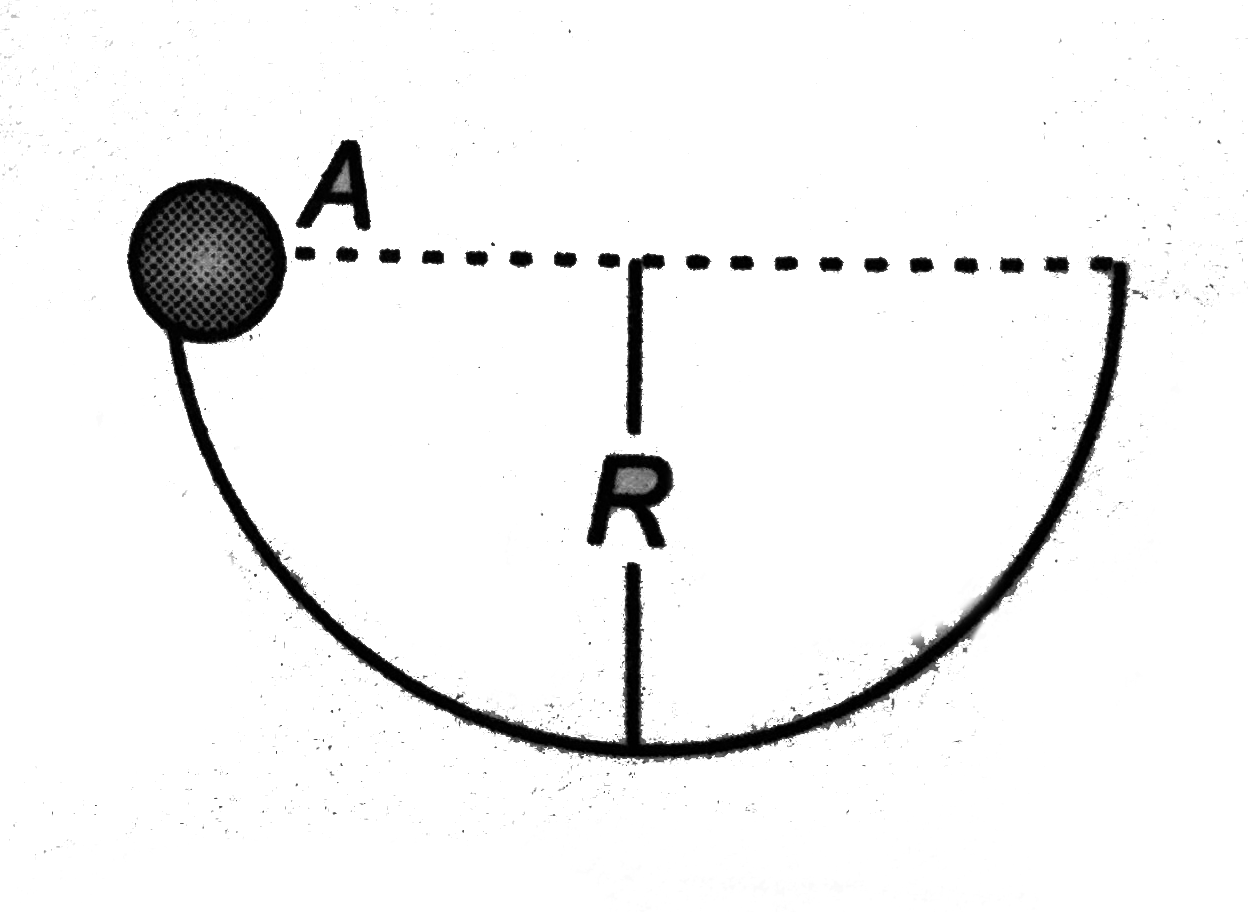
A small solid cylinder of radius r is released coaxially from point A inside the fixed large cylindrical bawl of radius R as shown in figure. If the friction between the small and the large cylinder is sufficient enough to prevent any slipping then find.
(a). What fractions of the total energy are translational and rotational when the small cylinder reaches the bottom of the larger one?
(b). The normal force exerted by the small cylinder on the larger one when it is at the bottom.
View Solution
Knowledge Check
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZero

A small solid cylinder of radius r is released coaxially from point A inside the fixed large cylindrical bawl of radius R as shown in figure. If the friction between the small and the large cylinder is sufficient enough to prevent any slipping then find.
(a). What fractions of the total energy are translational and rotational when the small cylinder reaches the bottom of the larger one?
(b). The normal force exerted by the small cylinder on the larger one when it is at the bottom.
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 π cm (Ice is lighter than water)
View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 π cm (Ice is lighter than water)
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionThe uniform cubical slab of side 'a' is released from rest in the position shown in the figure. For what value of 'x' is the angular acceleration maximum ( friction between the surface and cube is sufficient to prevent any slipping ?

View Solution
