A hemispherical cup of radius r with its centre of gravity at C distant c from its centre rests on the top of a spherical surface of radius R as shown in figure 6.15 .Assuming that there is sufficient friction to prevent slipping , establish the criterion of stablility of the cup in the position shown.

The correct Answer is:R>r(rc−1)
Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
Similar Questions
Locate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:

View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
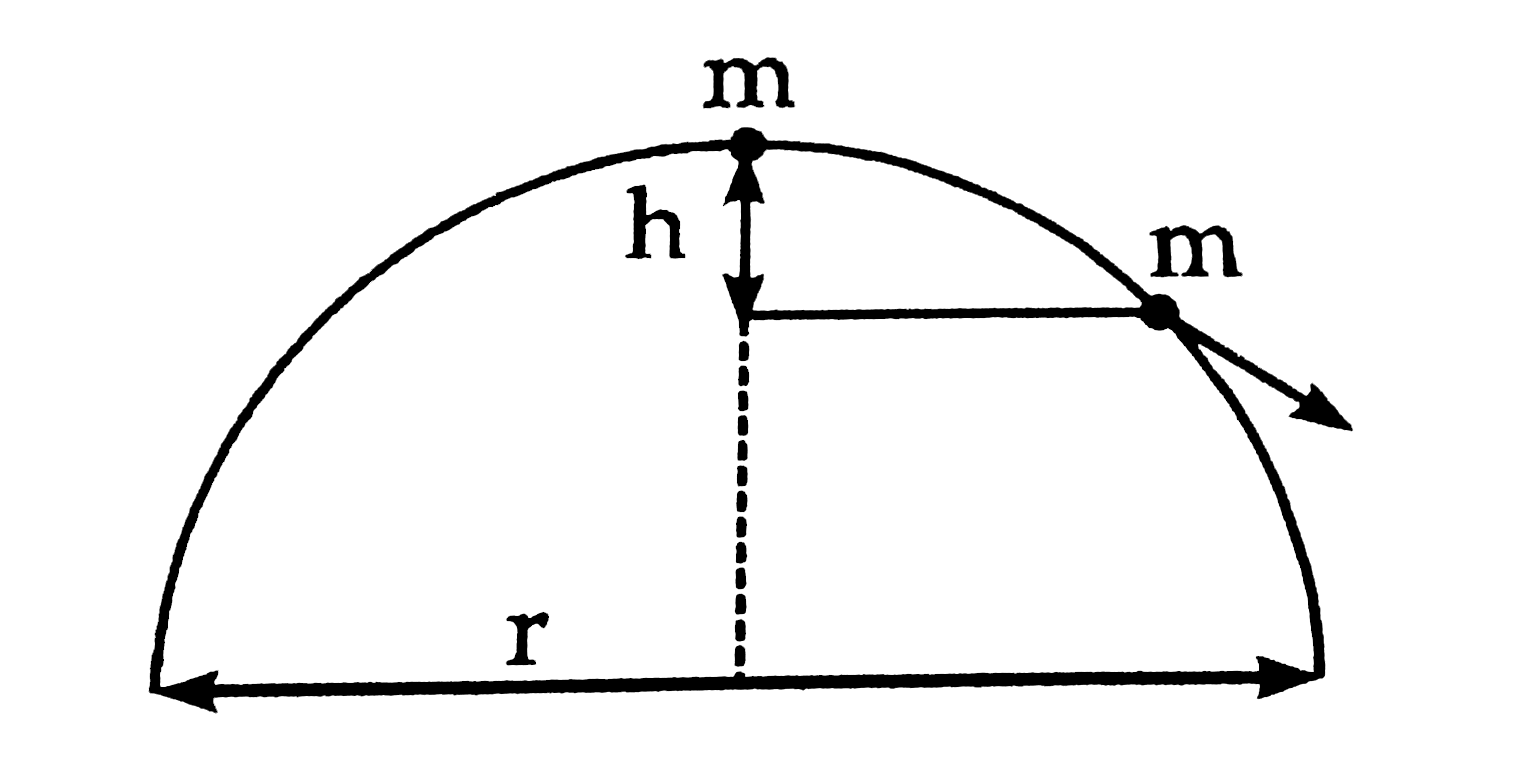
View Solution
Knowledge Check
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
 AF2 towards rightBF3 towards leftC2F3 towards rightDZero
AF2 towards rightBF3 towards leftC2F3 towards rightDZeroA charged spherical conductor of radius 10cm has potential V at a point distant 5cm from its centre. The potential at a point distant 15cm from the centre will be
A3VB32VC23VD13V
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionIf a charged spherical conductor of radius 10cm has potential V at a point distant 5cm from its centre, then the potential at a point distant 15cm from the centre will be
View SolutionA cube of uniform density and edge a is balanced on a cylindrical surface of radius r. Shown that the criterion for stability of equilibrium of the cube, assuming that fraction is sufficient to prevent slipping, is r>a/2
View SolutionThe dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
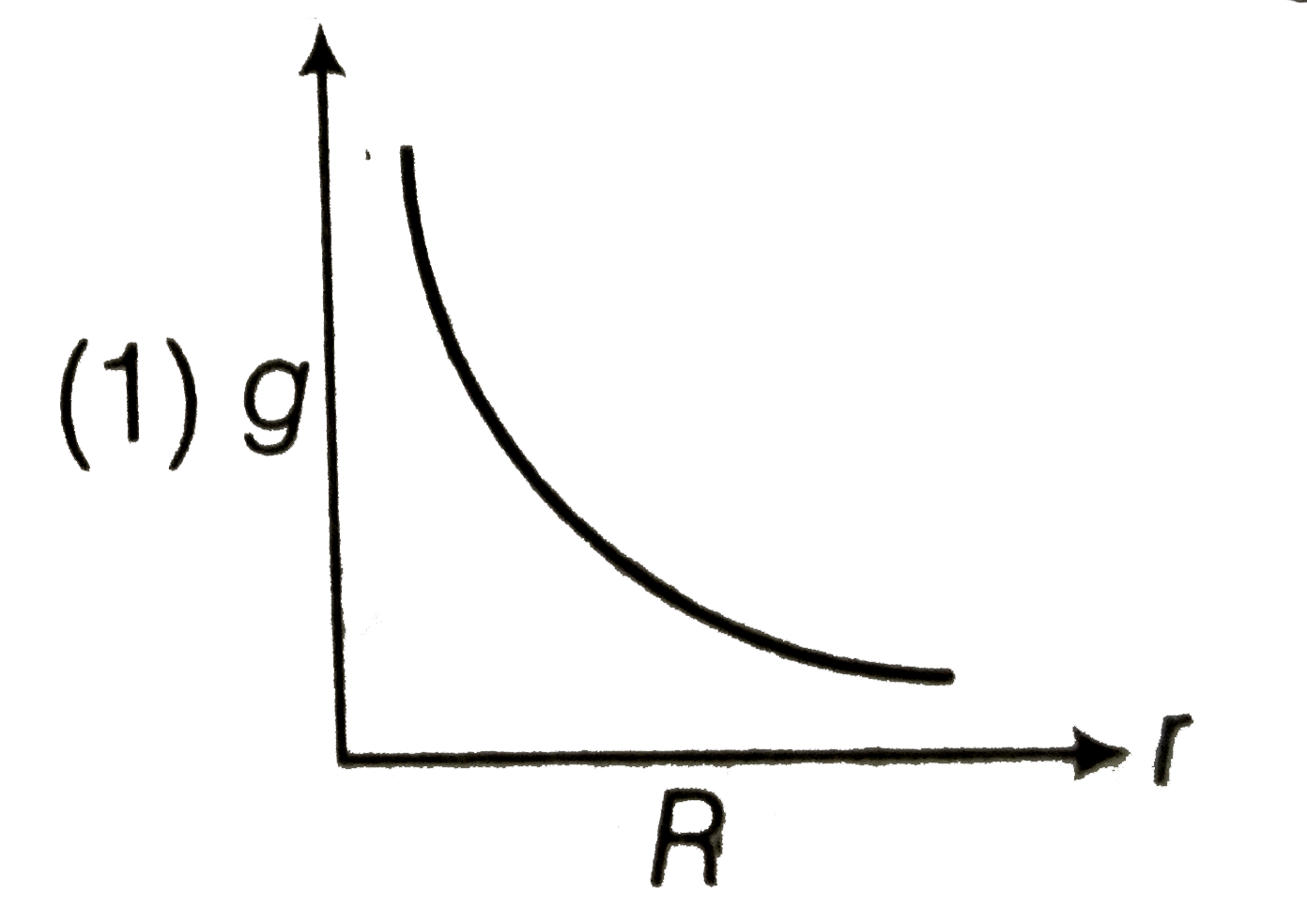
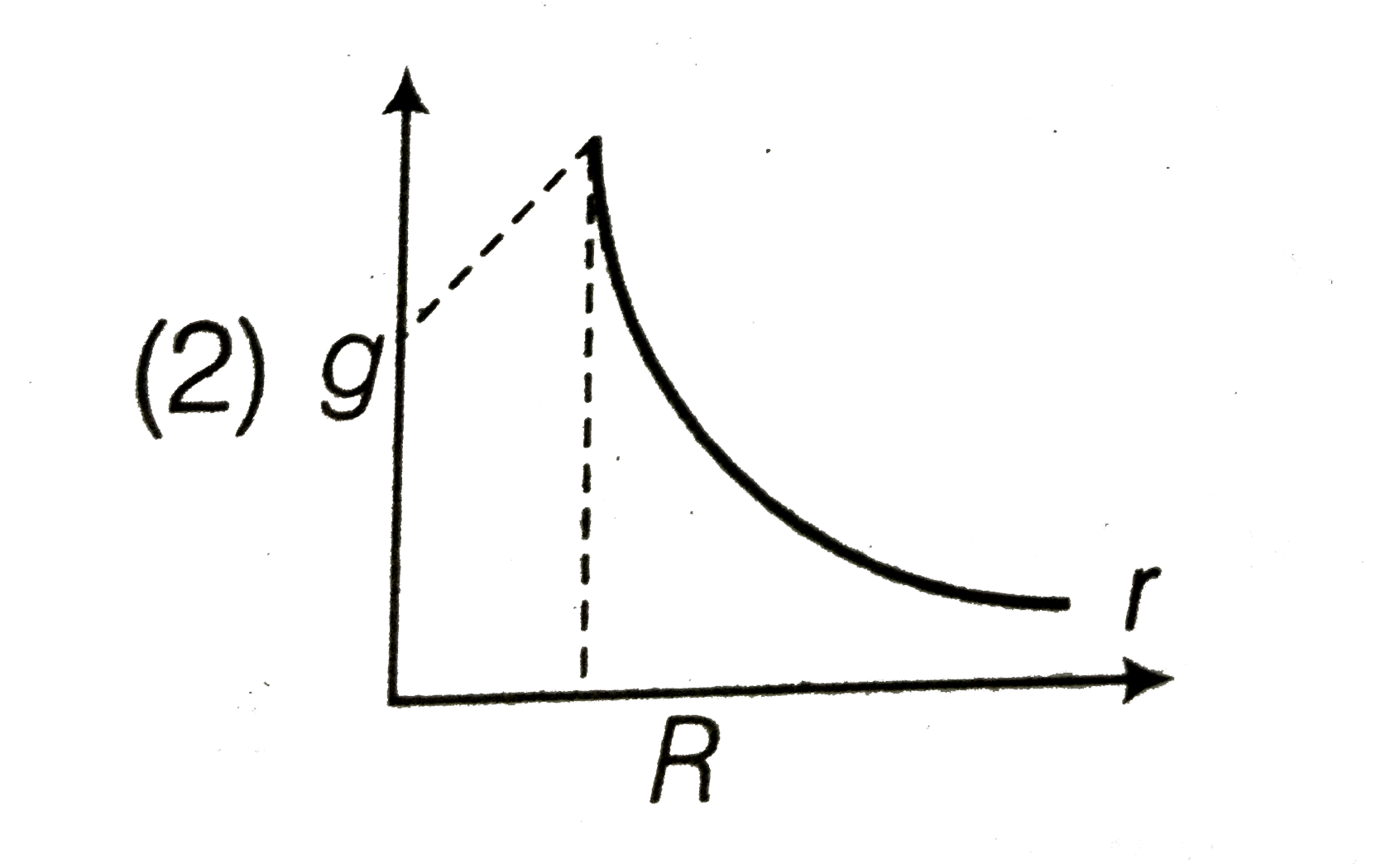
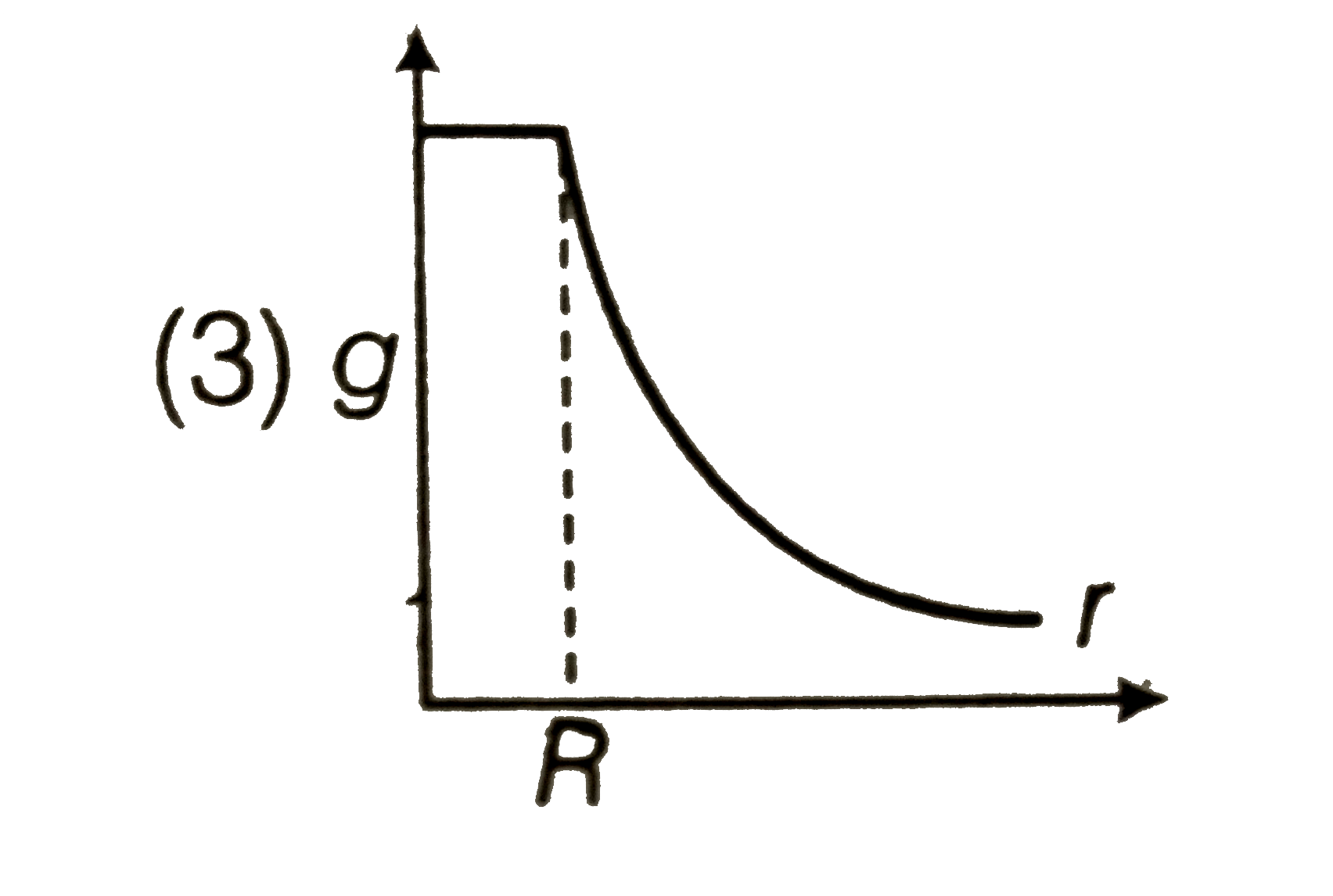
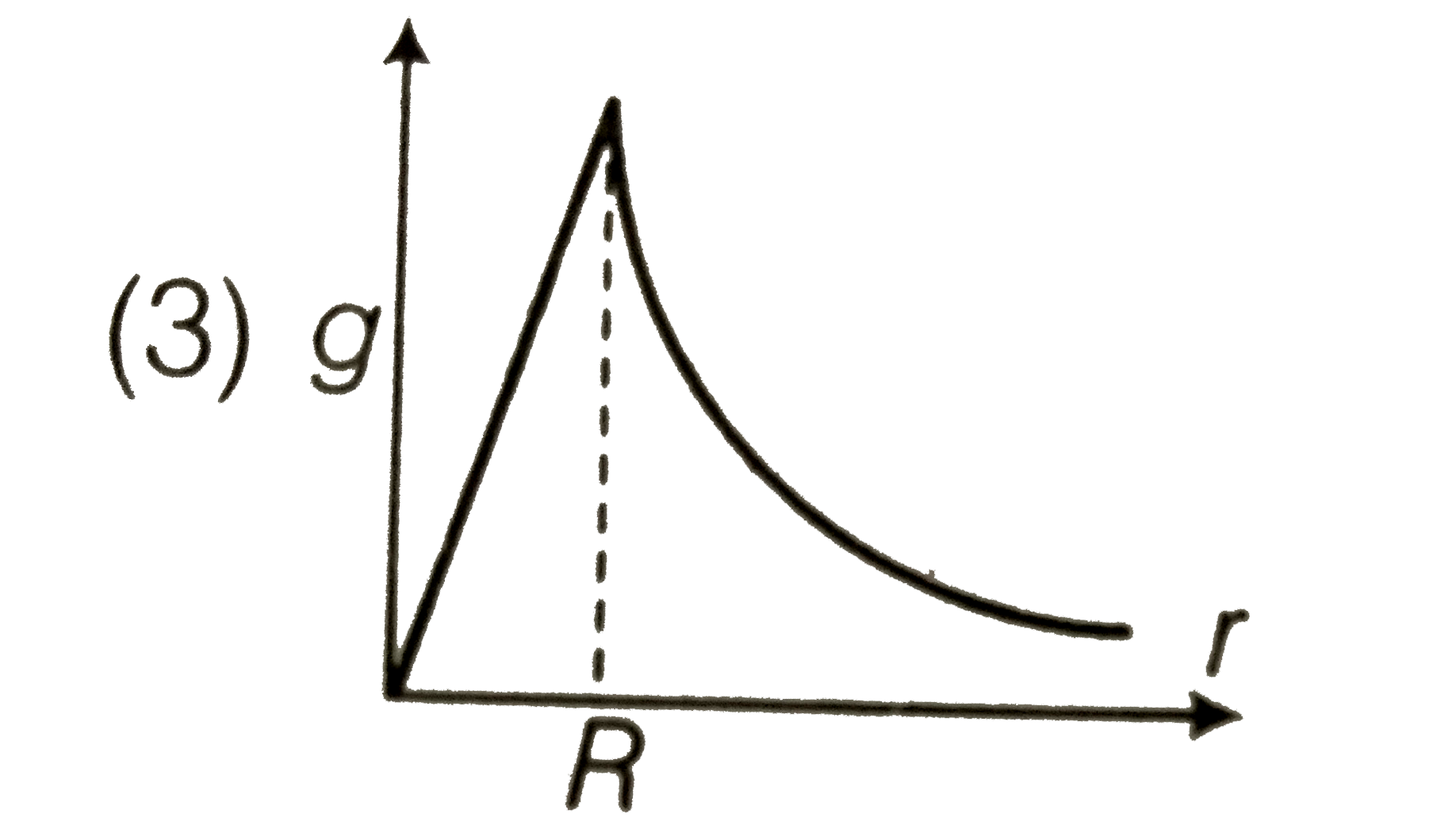
The correct figure is
View SolutionIf a charged spherical conductor of radius 10cm has potential V at a point distant 5cm from its centre, then the potential at a point distant 15cm from the centre will be
View Solution
