A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,Solution in Tamil
,Solution in Tamil
The specific gravity of the block =0.8. Hence the height inside water =3cm×0.8=2.4cm. The height outside water =3cm−2.4=0.6cm. Suppose the maximum weight that can be put without wetting it is W. The block in this case is completely immersed i the water. The volume of the displaced water
=volumeoftheblock=27xx10^-6m^3<br>Hencetheforceofbuoyacy.<br>=(27xx10^-6m^I3)xx(1000kgm^-3)(10ms^-2)<br>=0.27N<br>Thespr∈giscompressedby0.6cmandhencetheupwardfoceexertedbythespr∈g.<br>=50 Nm^-1xx0.6cm=0.3N<br>theforeceofbuoyancyandthespr∈gforcetaken→≥therbalancetheweightoftheblockplustheweightwputontheblock.Theweightoftheblockis<br>W'=(27xx10^-6m)xx(800kgm^-3)xx(10ms^-2)<br>=0.22N<br>Thus,W=0.27N+0.3N-0.22N<br>=0.35N
Topper's Solved these Questions
Similar Questions
Find the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionA body slipping on a rough horizontal plane moves wioth a deceleationof 4.0ms. What is cofficient of kineic friction between the block and the plane?
View SolutionFind the ratio of the weights as measured by a spring balance, of a 1 kg block of iron nd a 1kg block of wood. Density of iron =7800kgm−3 density of wood =800kgm−3anddensityofair=1.293kgm−3.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionIf the force constant of spring is 50Nm−1, find mass of the block, if it an rests in the given situation (g=10ms−2).

View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cubical block 'A' of mass m_(0)(=a^(3)rho=3 kg) of edge 'a' and density rho floats in a liquid of density 3rho . The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a^(2)rho g) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View Solution3 cm किनारे वाली लकड़ी का एक घन एक बरतन में रखे पानी में तैरता है | यह घन बरतन में रखे दो प्लेटों के बिच में है (चित्र 24. W4) जिसके कारण इसकी सतहें क्षैतिज तथा ऊर्ध्वाधर तलों में रहती है | इस बरतन की पेंदी में एक ऊर्ध्वाधर स्प्रिंग जुड़ा है | घन की निचली सतह स्प्रिंग के ऊपरी सिरे को छूती है | इस घन के ऊपर अधिकतम कितने भार की वस्तु रखी जा सकती है ताकि वह पानी में न भींगे ? लकड़ी का घनत्व =800kg/m3, स्प्रिंग नियतांक =50N/m,g=10m/s2.
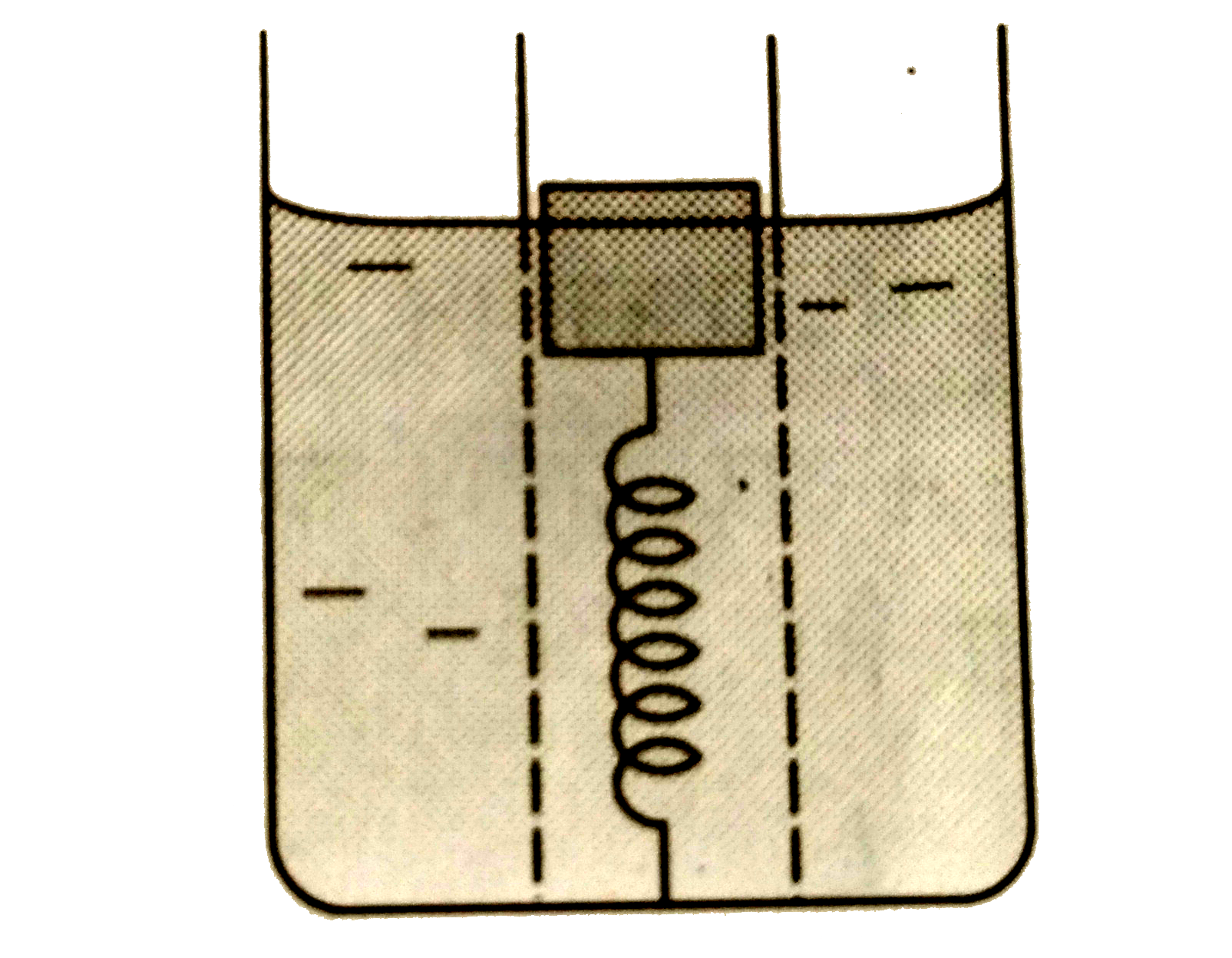
View SolutionA cubical wooden block of side 3 cm floats on water kept in a vessel. The lower face of the cube just touches the free end of a vertical spring fixed at the bottom of the vessel. Find the maximum weight that can be put on the block so that the weight does not touch water. The specific gravity of wood = 0.8 , the force constant of the spring = 50N*m^(-1)andg=10m*s^(-2) .
View SolutionA spring is attached to a wooden cubical block of edge 5cm and placed in a water conatiner as shown in figure. Calculate the maximum weight to be placed on the block so that it is just immersed in water completely. Density of wood =700kg/m3, spring constant of spring =70N/m,g=10m/s2. Assume that initially spring is in its normal length.

View SolutionFind the ratio of the weights, as measured by a spring balance, of a 1 kg block of iron and a 1kg block of wood. Density of iron =7800kgm−3 density of wood =800kgm−3 and density of air =1.293kgm−3.
View SolutionA block of mass .M. moving on the firctionless , horizontal surface collides with the spring of spring constant .k.. The other end of the spring is rigidly fixed to a vertical wall. If the spring is compressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View Solutionl Length and rho A cubic block of density 2rho K is floating in water. The bottom surface of the cuboid is attached to the free end of the massless spring in the bottom of the vessel. The force of the spring is constant k when w weight is placed on the block. Then it is completely immersed in liquid. Then the value of w will be
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
