A cubical wood piece of mass 13.5 gm and volume 0.0027m3 float in water. It is depressed and released, then it executes simple harmonic motion. Calculate the period of oscillation ?
The correct Answer is:0.0238 s
To solve the problem of finding the period of oscillation of a cubical wood piece floating in water, we will follow these steps:
Step 1: Identify the given data
- Mass of the wood piece, m=13.5g=0.0135kg (convert grams to kilograms)
- Volume of the wood piece, V=0.0027m3
- Density of water, ρwater=1000kg/m3
Step 2: Calculate the density of the wood
The density of the wood can be calculated using the formula:
ρwood=mV
Substituting the values:
ρwood=0.0135kg0.0027m3=5kg/m3
Step 3: Determine the equilibrium condition
When the wood piece is floating, the buoyant force equals the weight of the wood piece:
Fb=mg
Where Fb is the buoyant force and g is the acceleration due to gravity (approximately 9.81m/s2).
Step 4: Calculate the submerged volume
The buoyant force can also be expressed as:
Fb=ρwater⋅Vsubmerged⋅g
At equilibrium, we have:
ρwater⋅Vsubmerged⋅g=mg
From this, we can find Vsubmerged:
Vsubmerged=mgρwater⋅g=0.0135kg1000kg/m3=0.0000135m3
Step 5: Set up the equation of motion
When the block is depressed by a distance x, the additional buoyant force is given by:
F′b=ρwater⋅(Vsubmerged+A⋅x)⋅g
Where A is the cross-sectional area of the cube.
Step 6: Relate the forces to simple harmonic motion
The net force acting on the block when it is displaced is given by:
F=F′b−mg
This force will lead to simple harmonic motion, where:
F=−kx
Where k is the effective spring constant.
Step 7: Find the angular frequency ω
The angular frequency ω for simple harmonic motion is given by:
ω=√km
From the buoyant force relationship, we can derive:
k=ρwater⋅A⋅g
Thus,
ω=√ρwater⋅A⋅gm
Step 8: Calculate the period T
The period of oscillation T is given by:
T=2π√mk=2π√mρwater⋅A⋅g
Step 9: Substitute the values
Assuming the side length a of the cube is 0.3m:
A=a2=(0.3)2=0.09m2
Substituting the values:
T=2π√0.01351000⋅0.09⋅9.81
Calculating this gives:
T≈2.43s
Final Answer
The period of oscillation of the cubical wood piece is approximately T≈2.43s.
---
- Mass of the wood piece, m=13.5g=0.0135kg (convert grams to kilograms)
- Volume of the wood piece, V=0.0027m3
- Density of water, ρwater=1000kg/m3
The density of the wood can be calculated using the formula:
ρwood=mV
Substituting the values:
ρwood=0.0135kg0.0027m3=5kg/m3
When the wood piece is floating, the buoyant force equals the weight of the wood piece:
Fb=mg
Where Fb is the buoyant force and g is the acceleration due to gravity (approximately 9.81m/s2).
The buoyant force can also be expressed as:
Fb=ρwater⋅Vsubmerged⋅g
At equilibrium, we have:
ρwater⋅Vsubmerged⋅g=mg
From this, we can find Vsubmerged:
Vsubmerged=mgρwater⋅g=0.0135kg1000kg/m3=0.0000135m3
When the block is depressed by a distance x, the additional buoyant force is given by:
F′b=ρwater⋅(Vsubmerged+A⋅x)⋅g
Where A is the cross-sectional area of the cube.
The net force acting on the block when it is displaced is given by:
F=F′b−mg
This force will lead to simple harmonic motion, where:
F=−kx
Where k is the effective spring constant.
The angular frequency ω for simple harmonic motion is given by:
ω=√km
From the buoyant force relationship, we can derive:
k=ρwater⋅A⋅g
Thus,
ω=√ρwater⋅A⋅gm
The period of oscillation T is given by:
T=2π√mk=2π√mρwater⋅A⋅g
Assuming the side length a of the cube is 0.3m:
A=a2=(0.3)2=0.09m2
Substituting the values:
T=2π√0.01351000⋅0.09⋅9.81
Calculating this gives:
T≈2.43s
The period of oscillation of the cubical wood piece is approximately T≈2.43s.
Topper's Solved these Questions
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (FROM TIME PERIOD OF OSCILLATION OF A S.H. OSCILLATOR)
Explore 19 Videos
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
Explore 19 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
Explore 12 Videos
Similar Questions
Assume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
View SolutionConsider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
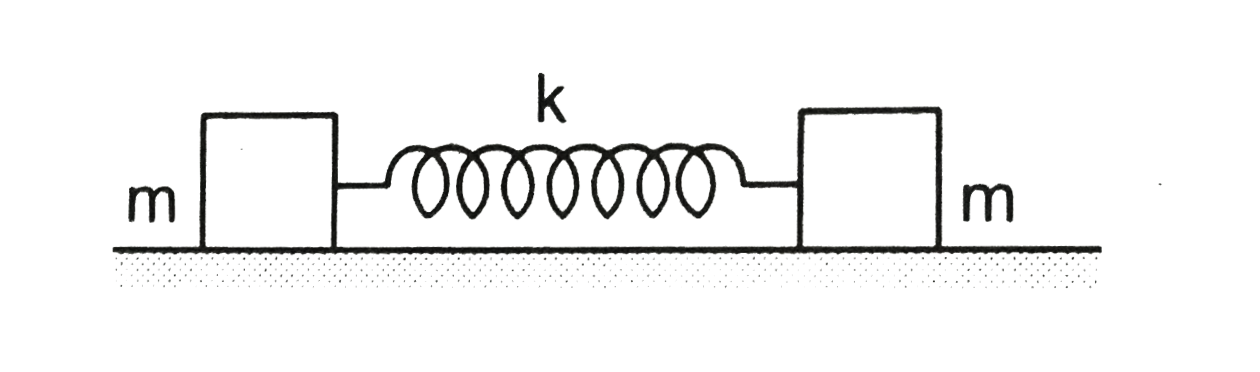
View Solution
Knowledge Check
The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
Consider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

View Solution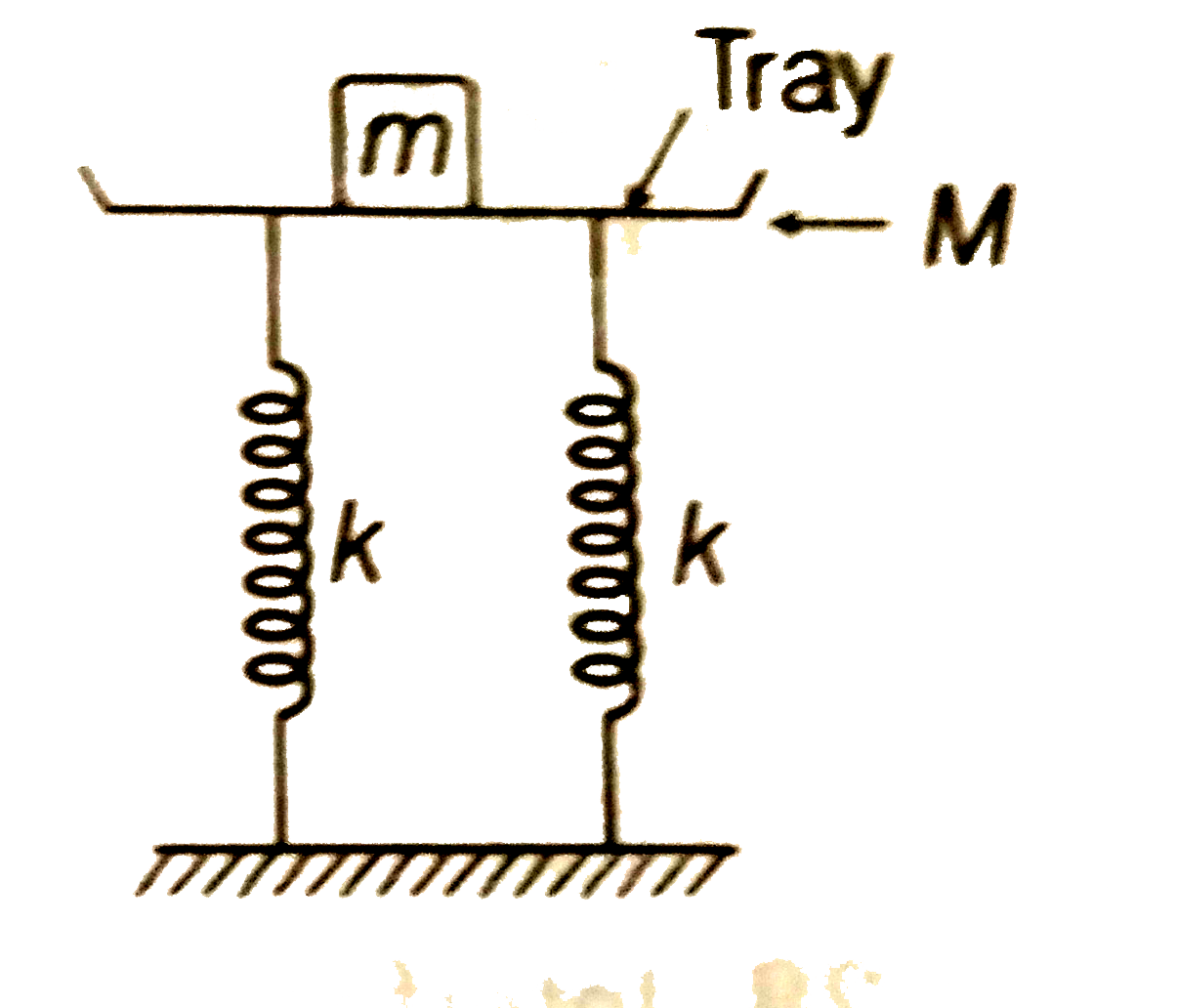
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a block of mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
View SolutionA cylindrical piece of cork of height 4.9 cm floats in water with its axis vertical and is made to execute slın. Calculate its time period of oscillation if its density is 0.2 gm/cc ?
View SolutionA body of mass m attached to one end of an ideal spring of force constant k is executing simple harmonic motion. Establish that the time - period of oscillation is T=2π√m/k.
View SolutionThe maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View Solution
