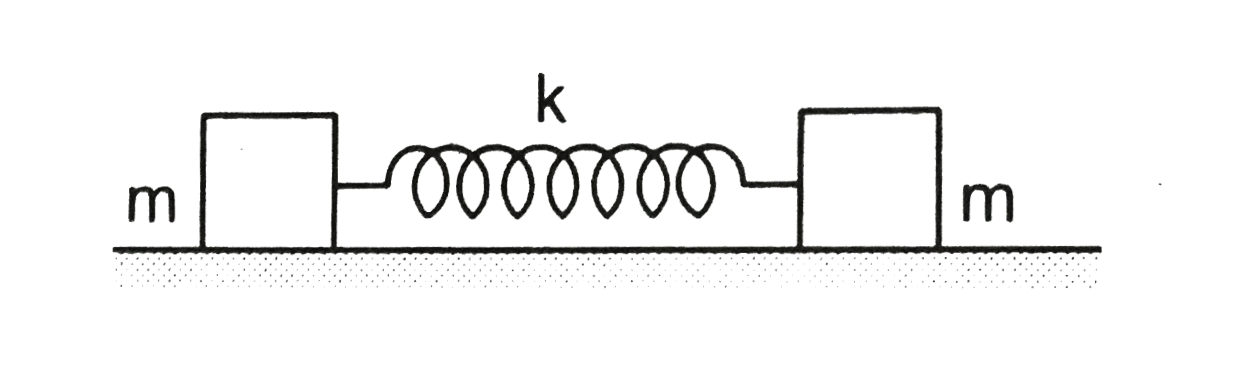
Consider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $T = 2 π \sqrt{\frac{m}{2 k}}$

The centre of mass of the system should not change during the motion.
So,if the block m on the left moves towards right a distance x the block on the right moves towards left a distance x so total compression of the spring is 2x.
By energy method
$\frac{1}{2} k {(2 x)}^{2} + \frac{1}{2} m v^{2} + \frac{1}{2} m v^{2} = C$
$\to m v^{2} + 2 k x^{2} = C$
Taking derivative of both sides with respect to t.
$m 2 v \frac{d v}{d t} + 2 k \times 2 x \frac{d x}{d t} = 0$
$∴ m a + 2 k x = 0$
[because $v = \frac{d x}{d t} and a = \frac{d v}{d t}]$
$\to - \frac{a}{x} = \frac{2 k}{m} ω^{2}$
$\to ω = \sqrt{\frac{2 k}{m}}$
$\to$ Time period
$T = 2 π \sqrt{\frac{m}{2 k}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The time period of simple harmonic motion depends upon
Aamplitude
Benergy
Cphase constant
Dmass

HC VERMA ENGLISH-SIMPLE HARMONIC MOTION-Exercises

Home
Ask Doubt
Profile