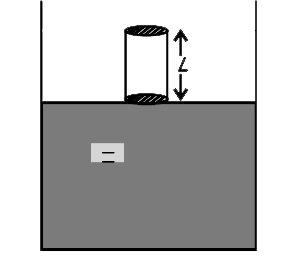
A cuboidal piece of wood has dimensions and . its relatively density is . it is floating in a large body of water such that side is vertical. It is pushed down a bit and released. The time period of SHM executed by it is
The correct Answer is:D
To find the time period of the simple harmonic motion (SHM) executed by the cuboidal piece of wood floating in water, we can follow these steps:
Step 1: Understand the Forces Acting on the Wood
When the wood is floating, it displaces a volume of water equal to its weight. The downward force (weight of the wood) is equal to the upward buoyant force (weight of the displaced water).
Step 2: Calculate the Weight of the Wood
The weight of the wood can be expressed as:
Fdown=mg=ρwood⋅V⋅g=d⋅(abc)⋅g
where d is the relative density of the wood, V is the volume of the wood, and g is the acceleration due to gravity.
Step 3: Calculate the Buoyant Force
The buoyant force acting on the wood is given by the weight of the displaced water:
Fup=ρwater⋅Vdisplaced⋅g=1⋅(bcY)⋅g
where Y is the depth of the submerged part of the wood.
Step 4: Set Up the Equilibrium Condition
At equilibrium, the downward force equals the upward force:
d⋅(abc)⋅g=(bcY)⋅g
Cancelling g from both sides, we have:
d⋅abc=bcY
From this, we can solve for Y:
Y=d⋅a1
Step 5: Determine the Amplitude of Motion
When the wood is pushed down and released, the maximum displacement from the mean position (equilibrium position) is:
A=a−Y=a−d⋅a=a(1−d)
Step 6: Calculate the Acceleration
The net force when the wood is displaced by a distance x from the mean position is given by:
Fnet=Fup−Fdown
This can be expressed as:
Fnet=(bc⋅(Y+x)⋅g)−(d⋅abc⋅g)
Substituting Y into the equation gives:
Fnet=(bc⋅(d⋅a+x)⋅g)−(d⋅abc⋅g)
This simplifies to:
Fnet=bcg⋅x
Step 7: Relate Force to Acceleration
Using Newton's second law, we can relate the net force to acceleration:
Fnet=m⋅a
where m=d⋅abc. Thus:
bcg⋅x=d⋅abc⋅a
Step 8: Find the Angular Frequency
The equation of motion for SHM can be written as:
a=−ω2x
From the above, we can derive:
ω2=bcgd⋅abc
Thus:
ω=√ga(1−d)
Step 9: Calculate the Time Period
The time period T of SHM is given by:
T=2πω=2π√a(1−d)g
Final Answer
The time period of SHM executed by the cuboidal piece of wood is:
T=2π√a(1−d)g
When the wood is floating, it displaces a volume of water equal to its weight. The downward force (weight of the wood) is equal to the upward buoyant force (weight of the displaced water).
The weight of the wood can be expressed as:
Fdown=mg=ρwood⋅V⋅g=d⋅(abc)⋅g
where d is the relative density of the wood, V is the volume of the wood, and g is the acceleration due to gravity.
The buoyant force acting on the wood is given by the weight of the displaced water:
Fup=ρwater⋅Vdisplaced⋅g=1⋅(bcY)⋅g
where Y is the depth of the submerged part of the wood.
At equilibrium, the downward force equals the upward force:
d⋅(abc)⋅g=(bcY)⋅g
Cancelling g from both sides, we have:
d⋅abc=bcY
From this, we can solve for Y:
Y=d⋅a1
When the wood is pushed down and released, the maximum displacement from the mean position (equilibrium position) is:
A=a−Y=a−d⋅a=a(1−d)
The net force when the wood is displaced by a distance x from the mean position is given by:
Fnet=Fup−Fdown
This can be expressed as:
Fnet=(bc⋅(Y+x)⋅g)−(d⋅abc⋅g)
Substituting Y into the equation gives:
Fnet=(bc⋅(d⋅a+x)⋅g)−(d⋅abc⋅g)
This simplifies to:
Fnet=bcg⋅x
Using Newton's second law, we can relate the net force to acceleration:
Fnet=m⋅a
where m=d⋅abc. Thus:
bcg⋅x=d⋅abc⋅a
The equation of motion for SHM can be written as:
a=−ω2x
From the above, we can derive:
ω2=bcgd⋅abc
Thus:
ω=√ga(1−d)
The time period T of SHM is given by:
T=2πω=2π√a(1−d)g
The time period of SHM executed by the cuboidal piece of wood is:
T=2π√a(1−d)g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A glass tube is floating in a liquid with 30 cm of its length immersed in the liquid. If the glass tube is pushed down and released, then calculate the time period of vibration of glass tube.
View Solution(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density 2ρ. A wooden cylinder of cross sectional area A and length L has density ρ. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.
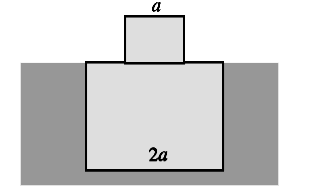
View Solution
Knowledge Check
A piece of wood has dimensions 'a', 'b' and 'c'. Its relative density is d. It is floating in water such that the side 'a' is vertical. It is now pushed down gently and relesed. The time-period of S.H.M. is
AT=2π√abcgBT=2π√bcdgCT=2π√gdaDT=2π√dagA pole is floating in a liquid with 80 cm of its length immersed. It is pushed doun a certain distance and then released. Time period of vertical oscillation is
A4π7sB3π7sC2π7sDπ7sA cylinderical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When dressed a little and the released the block starts oscillating. The period oscillations is
A(2π√mρbgB2π√mgρAC2π√ρAgmD2π√ρAmg)
A thin vertical tube of weight 12 g and external diameter 1 cm is made to float vertically in water by placing 12 g of mercury at its bottom. If the tube is depressed slightly and then released, determine the time period of S.H.M.
Take g=10m/s2
View SolutionA brass cube of side a and density σis floating in mercury of density ρ. If the cube is displaced a bit vertically, it executes S.H.M. Its time period will be
View SolutionA cube made of wood having specific gravity 0.4 and side length a is floated in a large tanck full of water.
If the cube is depressed slighly, it executes SHM from it's position. What is it's time period?
View SolutionA cube made of wood having specific gravity 0.4 and side length a is floated in a large tank full of water.
 If the cube is depressed slightly, it excutes SHM from It's position. What is it's time period?
If the cube is depressed slightly, it excutes SHM from It's position. What is it's time period?
View SolutionA solid sphere of density σ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
View Solution
