A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
The magnitude of magnetic moment now diminishes.
The magnetic moment does not change.
The magnitude of B at (0,0z), z>R increases.
The magnitude of B at (0,0,z), z>>R is unchanges.
The correct Answer is:A
To solve the problem, we need to analyze the magnetic moment and magnetic field of the current-carrying circular loop before and after it is bent. Here’s a step-by-step solution:
Step 1: Determine the initial magnetic moment of the loop
- The initial magnetic moment →M0 of a circular loop is given by the formula:
→M0=I⋅A
where I is the current and A is the area of the loop. The area A of a circular loop with radius R is:
A=πR2
Therefore, the initial magnetic moment is:
→M0=I⋅πR2^k
Step 2: Analyze the bending of the loop
- The loop is bent such that the part of the loop where x>0 is now in the y−z plane. The remaining part of the loop (where x<0) remains in the x−y plane.
Step 3: Calculate the new magnetic moment after bending
- The new configuration consists of two parts:
1. The semicircular part in the y−z plane.
2. The remaining semicircular part in the x−y plane.
- The magnetic moment for each semicircular part is:
- For the semicircular part in the y−z plane:
→M1=I⋅(πR22)(−^i)
- For the semicircular part in the x−y plane:
→M2=I⋅(πR22)^k
Step 4: Combine the magnetic moments
- The total magnetic moment →M after bending is:
→M=→M1+→M2=−I⋅πR22^i+I⋅πR22^k
Step 5: Calculate the magnitude of the new magnetic moment
- The magnitude of the new magnetic moment is given by:
|→M|=√(−I⋅πR22)2+(I⋅πR22)2
=√2(I⋅πR22)2=I⋅πR22√2
Step 6: Compare the new magnetic moment with the initial magnetic moment
- The initial magnetic moment was I⋅πR2, and the new magnetic moment is:
|→M|=I⋅πR2√2
- This shows that the new magnetic moment is less than the initial magnetic moment:
|→M|<|→M0|
Step 7: Calculate the magnetic field at point (0,0,z)
- The magnetic field →B0 at a point along the axis of the original loop is given by:
B0=μ04π⋅2IπR2(z2+R2)3/2^k
- After bending, the magnetic field →B at the same point is:
B=μ04π⋅IπR2(z2+R2)3/2(−^i)
Step 8: Compare the magnetic fields
- The magnitude of the magnetic field also decreases after bending:
|B|<|B0|
Conclusion
- The new magnetic moment decreases compared to the original magnetic moment.
- The magnetic field at the point (0,0,z) also decreases.
- The initial magnetic moment →M0 of a circular loop is given by the formula:
→M0=I⋅A
where I is the current and A is the area of the loop. The area A of a circular loop with radius R is:
A=πR2
Therefore, the initial magnetic moment is:
→M0=I⋅πR2^k
- The loop is bent such that the part of the loop where x>0 is now in the y−z plane. The remaining part of the loop (where x<0) remains in the x−y plane.
- The new configuration consists of two parts:
1. The semicircular part in the y−z plane.
2. The remaining semicircular part in the x−y plane.
- For the semicircular part in the y−z plane:
→M1=I⋅(πR22)(−^i)
- For the semicircular part in the x−y plane:
→M2=I⋅(πR22)^k
- The total magnetic moment →M after bending is:
→M=→M1+→M2=−I⋅πR22^i+I⋅πR22^k
- The magnitude of the new magnetic moment is given by:
|→M|=√(−I⋅πR22)2+(I⋅πR22)2
=√2(I⋅πR22)2=I⋅πR22√2
- The initial magnetic moment was I⋅πR2, and the new magnetic moment is:
|→M|=I⋅πR2√2
- This shows that the new magnetic moment is less than the initial magnetic moment:
|→M|<|→M0|
- The magnetic field →B0 at a point along the axis of the original loop is given by:
B0=μ04π⋅2IπR2(z2+R2)3/2^k
B=μ04π⋅IπR2(z2+R2)3/2(−^i)
- The magnitude of the magnetic field also decreases after bending:
|B|<|B0|
- The new magnetic moment decreases compared to the original magnetic moment.
- The magnetic field at the point (0,0,z) also decreases.
Topper's Solved these Questions
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - MCQs (More than one Options)
4 Videos
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Very Short Answer Type Question
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
- NUCLEIBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - NUCLEIEXERCISE - Long answer type question
10 Videos
Similar Questions
A current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the YZ− plane
View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA circular wire loop of radius R is placed in the x-y plane centered at the origin O. A square loop of side a(altltR) having two turns is placed with its centre at =√3R along the axis of hte circular wire loop, as shown in figure. The plane of the square loop makes an angle of 45∘ with respect to the z-axis. If the mutual inductance between the loops is given bu μ0a22p/2R, then the value of p is
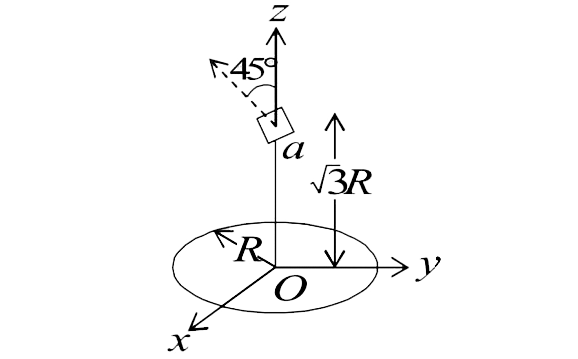
View SolutionA circular wire loop of radius R is placed in the x-y plane centered at the origin O. A square loop of side a(altltR) having two turns is placed with its centre at =√3R along the axis of hte circular wire loop, as shown in figure. The plane of the square loop makes an angle of 45∘ with respect to the z-axis. If the mutual inductance between the loops is given bu μ0a22p/2R, then the value of p is

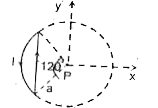
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA current carrying loop lies on a smooth horizontal plane. Then,
View Solution
