A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment →M
is non-zero and points in the z-direction by symmetry
points along the axis of the toroid (m=mϕ)
is zero, otherwise there would be a field falling as 1r3 at large distances outside the toroid
is pointing radially outwards.
The correct Answer is:C
To find the magnetic moment →M of a toroid with n turns, mean radius R, cross-sectional radius a, and carrying current I, we can follow these steps:
Step 1: Understand the Structure of the Toroid
A toroid is essentially a circular loop of wire that is bent into a donut shape. It consists of multiple turns (or loops) of wire, each carrying the same current I.
Step 2: Calculate the Area of Each Current Loop
The area A of each circular loop can be calculated using the formula for the area of a circle:
A=πa2
where a is the cross-sectional radius of the toroid.
Step 3: Calculate the Magnetic Moment of Each Loop
The magnetic moment dM of a single loop can be expressed as:
dM=I⋅A
Substituting the area from Step 2:
dM=I⋅(πa2)=Iπa2
Step 4: Calculate the Total Magnetic Moment for All Turns
Since there are n turns in the toroid, the total magnetic moment M can be calculated by multiplying the magnetic moment of one loop by the number of turns:
M=n⋅dM=n⋅(Iπa2)=nIπa2
Step 5: Consider the Direction of the Magnetic Moment
The direction of the magnetic moment for each loop is perpendicular to the plane of the loop. However, in a toroid, the loops are arranged such that the magnetic moments of diametrically opposite loops point in opposite directions.
Step 6: Analyze the Cancellation of Magnetic Moments
Due to the symmetry of the toroid, the magnetic moments of diametrically opposite loops cancel each other out. Therefore, when you sum up all the magnetic moments, they effectively cancel out, leading to a total magnetic moment of:
M=0
Final Result
Thus, the net magnetic moment →M of the toroid is:
→M=0
A toroid is essentially a circular loop of wire that is bent into a donut shape. It consists of multiple turns (or loops) of wire, each carrying the same current I.
The area A of each circular loop can be calculated using the formula for the area of a circle:
A=πa2
where a is the cross-sectional radius of the toroid.
The magnetic moment dM of a single loop can be expressed as:
dM=I⋅A
Substituting the area from Step 2:
dM=I⋅(πa2)=Iπa2
Since there are n turns in the toroid, the total magnetic moment M can be calculated by multiplying the magnetic moment of one loop by the number of turns:
M=n⋅dM=n⋅(Iπa2)=nIπa2
The direction of the magnetic moment for each loop is perpendicular to the plane of the loop. However, in a toroid, the loops are arranged such that the magnetic moments of diametrically opposite loops point in opposite directions.
Due to the symmetry of the toroid, the magnetic moments of diametrically opposite loops cancel each other out. Therefore, when you sum up all the magnetic moments, they effectively cancel out, leading to a total magnetic moment of:
M=0
Thus, the net magnetic moment →M of the toroid is:
→M=0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question
10 Videos
- MOVING CHARNGES AND MAGNETISMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions
7 Videos
Similar Questions
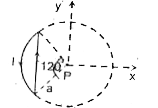
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil of radius 10cmand100 turns carries a current 1A. What is the magnetic moment of the coil?
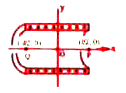
View SolutionA solenoid of length 'l' has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'P'(only axial component).
View Solution
