A current coil of total resistance R is kept inside magnetic field. How is the change in magnetic flux through the coil related to the amount of charge passing through the coil?
The correct Answer is:Δq=ΔϕR
To find the relationship between the change in magnetic flux through a coil and the amount of charge passing through the coil, we can follow these steps:
Step 1: Understand the relationship between EMF and magnetic flux
The electromotive force (EMF) induced in the coil due to a change in magnetic flux is given by Faraday's law of electromagnetic induction:
E=−dΦdt
where E is the EMF, Φ is the magnetic flux, and t is time.
Step 2: Relate EMF to current and resistance
According to Ohm's law, the relationship between EMF, current (I), and resistance (R) is given by:
E=I⋅R
Step 3: Express current in terms of charge
Current can also be defined as the rate of flow of charge:
I=dQdt
where Q is the charge.
Step 4: Substitute current into the EMF equation
From the previous steps, we can substitute I into the EMF equation:
E=dQdt⋅R
Step 5: Combine the equations
Now, we can equate the two expressions for EMF:
−dΦdt=dQdt⋅R
Step 6: Rearrange to find the relationship between charge and magnetic flux
Rearranging the equation gives:
dQ=−dΦdt⋅R⋅dt
This implies:
dQ=−R⋅dΦdt⋅dt
Step 7: Simplifying the relationship
If we consider a small time interval, we can express the total charge Q that has passed through the coil as:
Q=−R⋅ΔΦ
where ΔΦ is the change in magnetic flux over the time interval.
Final Relationship
Thus, the relationship between the change in magnetic flux through the coil and the amount of charge passing through the coil is:
ΔQ=−R⋅ΔΦ
The electromotive force (EMF) induced in the coil due to a change in magnetic flux is given by Faraday's law of electromagnetic induction:
E=−dΦdt
where E is the EMF, Φ is the magnetic flux, and t is time.
According to Ohm's law, the relationship between EMF, current (I), and resistance (R) is given by:
E=I⋅R
Current can also be defined as the rate of flow of charge:
I=dQdt
where Q is the charge.
From the previous steps, we can substitute I into the EMF equation:
E=dQdt⋅R
Now, we can equate the two expressions for EMF:
−dΦdt=dQdt⋅R
Rearranging the equation gives:
dQ=−dΦdt⋅R⋅dt
This implies:
dQ=−R⋅dΦdt⋅dt
If we consider a small time interval, we can express the total charge Q that has passed through the coil as:
Q=−R⋅ΔΦ
where ΔΦ is the change in magnetic flux over the time interval.
Thus, the relationship between the change in magnetic flux through the coil and the amount of charge passing through the coil is:
ΔQ=−R⋅ΔΦ
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS22videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - TOUGH & TRICKY PROBLEMS14videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
Similar Questions
A current-carrying coil of total resistance R is kept inside magnetic field. How is the change in magnetic flux through the coil related to the amount of charge passing through the coil ?
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
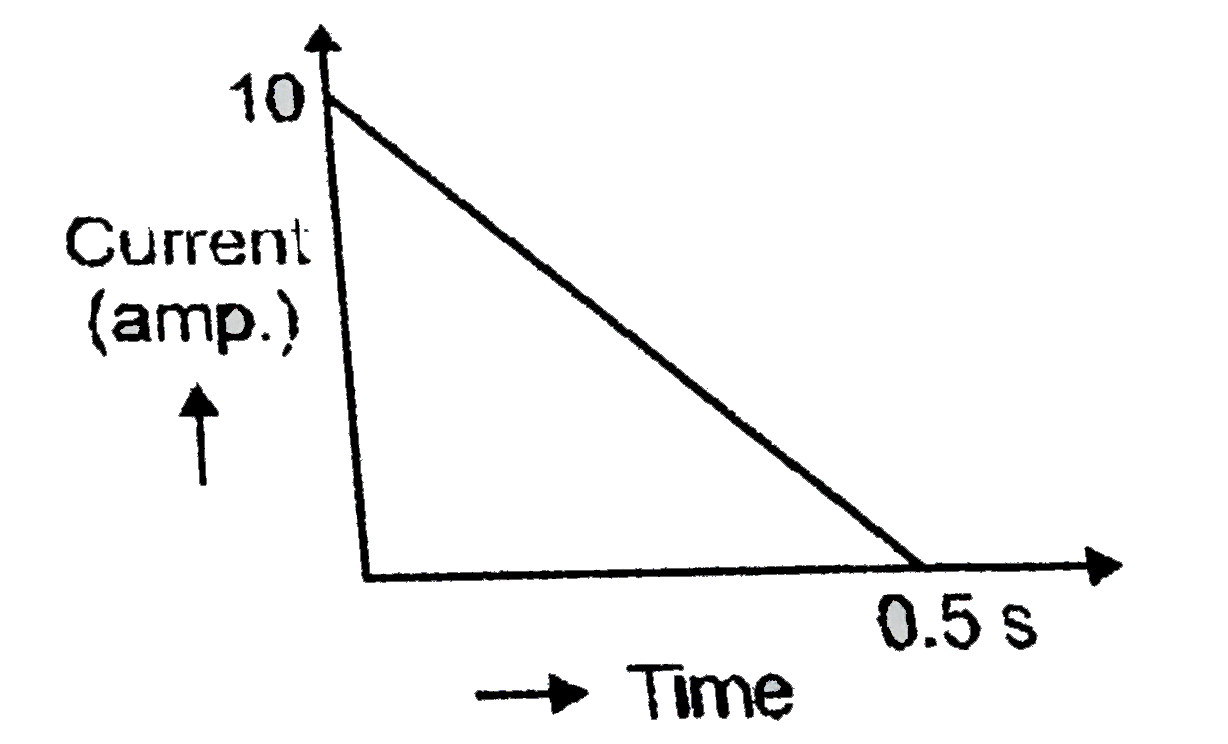 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Magnetic flux through a coil depends upon
Anumber of turnsBareaCmagnetic fieldDall of these - Question 2 - Select One
A resistance coil is held horizontally and a magnet is allowed to fall vertically through it . Then the acceleration of the magnet while passing through the coil is
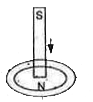 Aequal to gBless than gCmore than gDsometimes less and sometimes more than g
Aequal to gBless than gCmore than gDsometimes less and sometimes more than g - Question 3 - Select One
In a coil of resistance 50 W, the induced current developed by changing magnetic flux through it, is shown in figure as a function of time. The magnitude of change in flux through the coil is
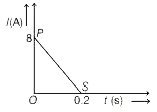 A10 WbB20 WbC32 WbD40 Wb
A10 WbB20 WbC32 WbD40 Wb
How magnetic flux generated in a coil depends on the current flowing through it?
View SolutionAssertion (A): Induced current in a coil is maintained only by a change in magnetic field.
Reason (R): The presence of large magnetic flux through a coil maintains a current in the coil if the circuit is continuous.View SolutionThe formula for induced e.m.f. in a coil due to change in magnetic flux through the coil is (here A = area of the coil, B = magnetic field)
View SolutionIn a coil of resistance 10 ohm , the induced current developed by changing magnetic flux through it, is shown in figure as a function of time . The magnitude of change in flux through the coil (in weber) is __
 View Solution
View SolutionA coil of resistance 400Ω is placed in a magnetic field. If the magnetic flux ϕ (wb) linked with the coil varies with time t (sec) as f=50t2+4, the current in the coil at t=2 sec is
View Solution

