A current I flows in a conducting wire of lenth L. If we bent it in a circular form, then calculate its magnetic dipole moment.
lL24πAm2
l2L4πAm2
lL22πAm2
l2L2πAm2
The correct Answer is:A
Let a wire of length L is bent in a circular form of radius r.
Then , 2πr=Limpliesr=L2π .......... (i)
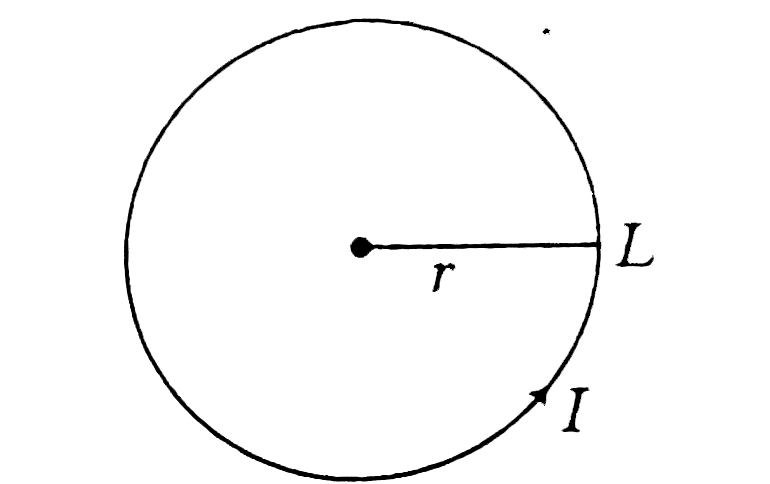
The magnetic dipole moment of a circular ring, M=lA ( where , A is area of the ring )
or M=lπr2 ............ (ii)
On putting the value of r from Eq. (i) in Eq. (ii) , we get
M=lπ(L2π)2
⇒M=lπ×L24π2
⇒M=lL24πA−m2
Topper's Solved these Questions
- MAGNETISM-IIBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETISM-IIEXERCISE - Exercise 2
12 Videos
- MAGNETISM-IIBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETISM-IIEXERCISE - MHT CET Corner
8 Videos
- MAGNETISM-IIBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETISM-IIEXERCISE - MHT CET Corner
8 Videos
- MAGNETISM-IBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETISM-IEXERCISE - Exercise 2
25 Videos
- MEASUREMENTSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MEASUREMENTSEXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS)
17 Videos
Similar Questions
One of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionA thin bar magnet has dipole moment M . If this is bent in the form of semicircle , then find the new dipole moment .
View Solution
Knowledge Check
A current I is flowing in a conductor of length L when it is bent in the form of a circular loop its magnetic moment
AIL4πB4πIL2C4πIL2DIL24πA steady current flows in a long wire. It is bent into a circular loop of one turn and the magnetic field at the center of the coil is B. If the same wire is bent into a circular loop of n turns, the magnetic field at the center of the coil is
ABnBnBCnB2Dn2BA magnet with moment M is given. If it is bent into a semicircular form, its new magnetic moment will be:
AM/πBM/2CMD2M/π
A steel wire of length l has a magnetic moment M. It is bent into a semicircular arc. What is the new magnetic moment?
View SolutionA magnetised steel wire of length L has a magnetic moment of 3.14Am2. If the wire is bent into a semicircular arc, then what would be its new magnetic moment? (assume that the poles are situated at the ends of the wire.)
View SolutionA magnetised steel wire of length L has a magnetic moment of 3.14Am2. If the wire is bent into a semicircular arc, then what would be its new magnetic moment? (assume that the poles are situated at the ends of the wire.)
View SolutionA wire of length l meter carrying current i ampere is bent in form of circle. Magnetic moment is
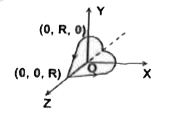
View SolutionA circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
View Solution
