A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius R1 and outer radius R2. Magnetic field B varies with distance r form the axis of the cylinder is

The correct Answer is:A
To find the magnetic field B at a distance r from the axis of a long hollow cylindrical wire with inner radius R1 and outer radius R2, we can use Ampere's Law, which states:
∮B⋅dl=μ0Iinside
where Iinside is the current enclosed by the Amperian loop.
Step 1: Analyze the regions
1. Region 1: r<R1 (inside the hollow part)
- There is no current enclosed.
- By Ampere's Law:
∮B⋅dl=0⟹B=0
2. Region 2: R1<r<R2 (within the hollow cylinder)
- Here, we need to find the current enclosed by a circular Amperian loop of radius r.
- The current density J is given by:
J=Iπ(R22−R21)
- The area of the annular region from R1 to r is:
A=π(r2−R21)
- The current enclosed by the Amperian loop is:
Iinside=J⋅A=Iπ(R22−R21)⋅π(r2−R21)=I(r2−R21)R22−R21
- By applying Ampere's Law:
B⋅(2πr)=μ0Iinside⟹B⋅(2πr)=μ0I(r2−R21)R22−R21
- Thus,
B=μ0I(r2−R21)2πr(R22−R21)
3. Region 3: r≥R2 (outside the hollow cylinder)
- The total current I is enclosed.
- By Ampere's Law:
B⋅(2πr)=μ0I⟹B=μ0I2πr
Summary of Results
- For r<R1:
B=0
- For R1<r<R2:
B=μ0I(r2−R21)2πr(R22−R21)
- For r≥R2:
B=μ0I2πr
- There is no current enclosed.
- By Ampere's Law:
∮B⋅dl=0⟹B=0
- Here, we need to find the current enclosed by a circular Amperian loop of radius r.
- The current density J is given by:
J=Iπ(R22−R21)
- The area of the annular region from R1 to r is:
A=π(r2−R21)
- The current enclosed by the Amperian loop is:
Iinside=J⋅A=Iπ(R22−R21)⋅π(r2−R21)=I(r2−R21)R22−R21
- By applying Ampere's Law:
B⋅(2πr)=μ0Iinside⟹B⋅(2πr)=μ0I(r2−R21)R22−R21
- Thus,
B=μ0I(r2−R21)2πr(R22−R21)
- The total current I is enclosed.
- By Ampere's Law:
B⋅(2πr)=μ0I⟹B=μ0I2πr
B=0
- For R1<r<R2:
B=μ0I(r2−R21)2πr(R22−R21)
- For r≥R2:
B=μ0I2πr
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A long staright wire of radius a carries a steady current I. The curent is unifromly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
View SolutionA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
View SolutionA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
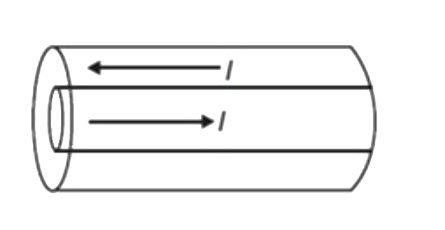
View SolutionThe figure shows a long coaxial cable in which a current I flows down through the inner cylinder of radius a and the same current flows back up through the outer cylinder of radius 2a. The cylinders are insulated from each other and the current is uniformly distributed over the area of the cross-section in each cylinder. The strength of the magnetic field at a distance 3a/2 from the axis of the cable is
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Draw graph of magnetic field B versus r (where r is distance from the axis of the wire)
View SolutionA long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
View SolutionA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
View SolutionA hollow cylinder with inner radius R. Outer radius 2R mass M is rolling with speed of it's axis v. What is its kinetic energy ?
 .
.
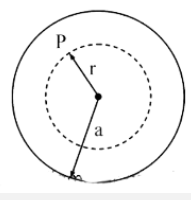
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
View Solution
