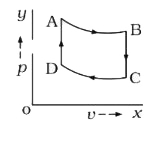
A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
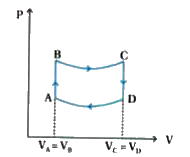
A to B: volume constant
B to C: adiabatic
C to D: volume constant
D to A: adiabatic
VC=VD=2VA=2VB
(a) In which part of the cycle heat is supplied to the engine from outside ?
(b) In which part of the cycle heat is being given to the surrounding by the engine ?
(c) What is the work done by the engine in one cycle ? Write your answer in term of PA,PB,VA
(d) What is the efficiency of the engine ? (γ=53 for the gas , CV=32R for one mole ) Solution in Gujrati
(a) For the process A to B, volume is constant
So, dV = 0 ∴ dW = 0
From first law of thermodynamics in,
dQ = dU + đW, dW = 0
∴ dQ=dU
Hence, in this process heat supplied is utilised to increases internal energy of the system.
As pressure is increased at constant volume (From Gay-Lussac.s law) i.e. P∝ T and internal energy is proportional to temperature and hence internal energy increases with temperature ∴dU>0
∴ From dQ=dU, dQ > 0 , so in process AB heat is supplied to the system.
(b)From dQ = dU, dQ > 0, so in process AB heat is supplied to the system. (b) In CD process, volume remains constant but pressure decreases. Hence, from P∝ T, temperature also decreases so heat is being given to the surrounding by the engine.
(c) To calculate work done by the engine in one cycle , we should calculate work done in each part separately.
∴WAB=∫PAPdV=0 ...(1)
WCD=∫VDVCPdV=0...(2)
WBC=∫VCVBPdV=K∫VCVBdVVγ=K1−γ[V1−γ]VCVB
=11−γ[PV]VCVB (adiabatic)
=PCVC−PBVB1−γ...(3)
Similarly , WDA=PAVA−PDVD1−γ (adiabatic) ...(4)
B and C are along adiabatic curve BC,
∴PBVγB=PCVγC
∴PC=PB(VBVC)γ=PB(12)γ=2−γPB...(5)
Similarly, PD=2−γPA ...(6)
Total work done by the engine in one cycle ABCDA
W=WAB+WBC+WCD+WDA
=0+WBC+0+WDA
W=11−γ(PCVC−PBVB)+11−γ(PAVA−PDVD)
W=11−γ[2−γPB(2VB)−PBVB]+11−γ[PAVA−2−γPA(2VA)]
W=11−γ[PBVB2−γ+1−PBVB+PAVA−2−γ+1PAVA]
∴W=11−γ[PBVB(2γ−1−1)−PAVA(21−γ−1)] but VA=VB
∴W=21−γ−11−γ[PBVA−PAVA]
=21−γ−11−γVA(PB−PA)
Putting γ=53 and simplifying
W=32⎡⎣1−(12)23⎤⎦(PB−PA)VA
(D) Efficiency η=Net workHeat supplied
=32[1−(12)23](PB−PA)VA32(PB−PA)VA
=⎡⎣1−(12)23⎤⎦
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-E MCQs42videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-F Questions from Module20videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Section-D Ncert Exemplar Solution (Short Answer )6videos
THERMODYANMICS
- BOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks1videos
THERMAL PROPERTIES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - UNITS AND MEASUREMENTEXERCISE - Section -F (Questions from Module )20videos
UNITS AND MEASUREMENT
Similar Questions
Heat absorbed by the gas undergo a cylic process along closed path in one complete cycle as shown in figure will be _____ J.
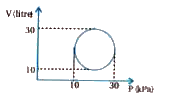 14:21View Solution
14:21View SolutionIn a thermodynamics process which one of the following statement is not true ?
06:41View SolutionConsider a Carnot's cycle operating between T1 = 500 K and T2 = 300 K producing 1 kJ of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.
05:57View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
02:01View SolutionIf the error in measurement of radius of a shpere is 2% then the error in determination of volume of the sphere will be …………
View SolutionA cycle followed by an engine (made of one mole of perfect gas in a cyclinder with a piston) is shown in (figure) A to B: volume constant B to C: adiabatic C to D: volume constant D to A: adiabatic V_(c)=V_(D)= 2V_(A)= 2V_(B) (a) In which part of the cycle heat is supplied to the engine fron outside? (b) In which part of the cycle heat is being given to the surrounding by the engine? (c ) What is the work done by the engine in one cycle? Write your answer in term of P_(A), P_(B), V_(A) . (d) What is the efficiency of the engine? (gamma= 5//3 "for the gas") , (C_(v)=3/2R "for one mole")
09:43View SolutionA cycle followed by an engine (made of one mole of an ideal gas in a cyclinder with a piston) is shown in (figure). Find heat exchanged by the engine, with the surrounding for each section of the cycle. [C_(V)= (3//2)R] AB : constant volume BC : constant pressure CD : adiabatic DA : constant pressure.
07:50View SolutionA cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.
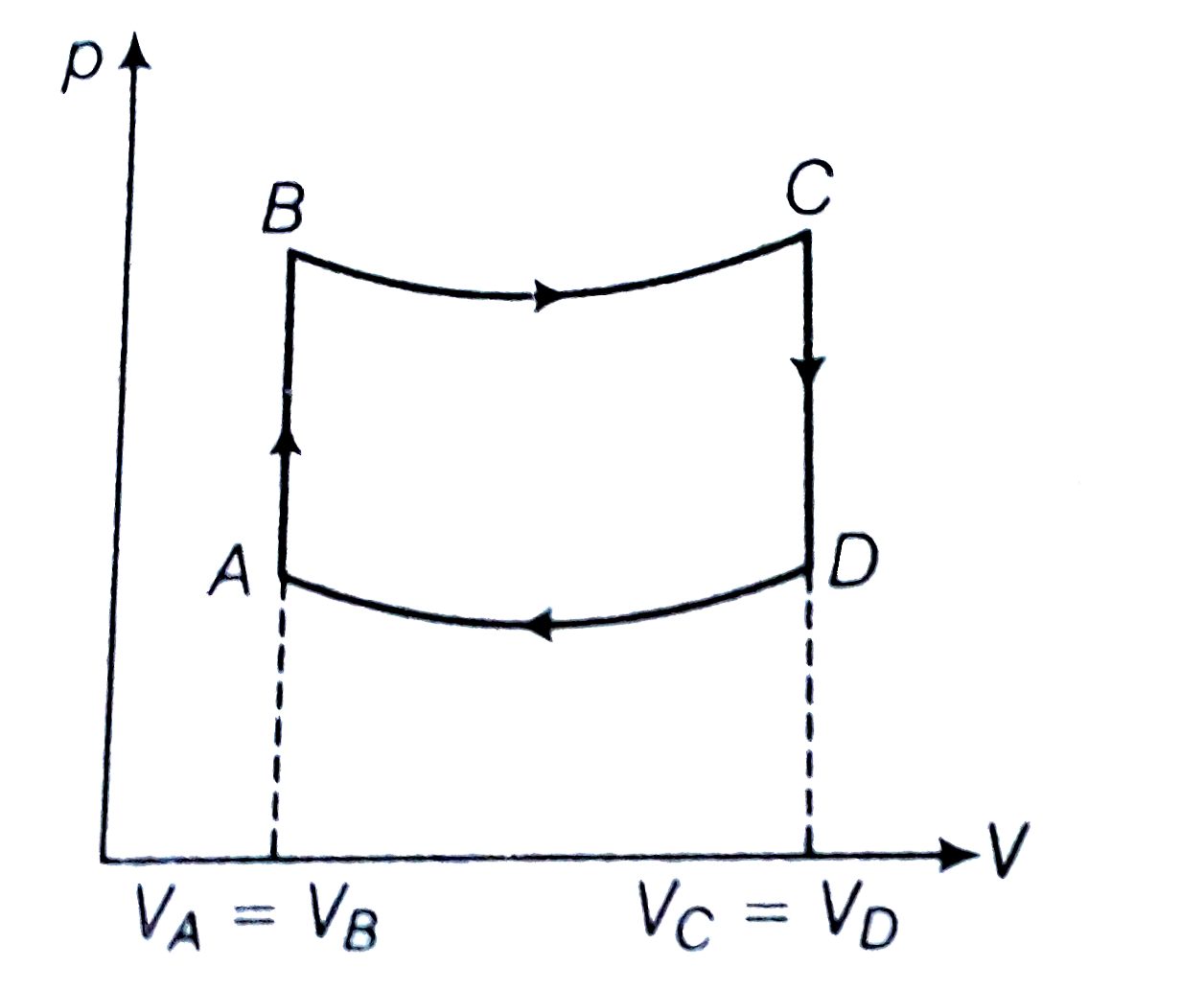
A to B volume constant, B to C adiabatic, C to D volume constant and D to A adiabatic
VC=VD=2VA=2VB
(a) In which part of the cycle heat is supplied to the engine form outside?
(b) In which part of the cycle heat is being given to the surrounding by the engine ?
(c ) What is the work done by the engine in one cycle ? Write your answer in term of pA,pB,VA ?
(d) What is the efficiency of the engine ?
(γ=53 for the gas), (CV=32R for one mole )14:16View SolutionThe cycle in the figure followed by an engine made of an ideal gas in ca cylinder with a piston, the heat exchanged by the engine with the surroundings for adiabatic section AB of cycle is (C_(V)=(3)/(2)R)
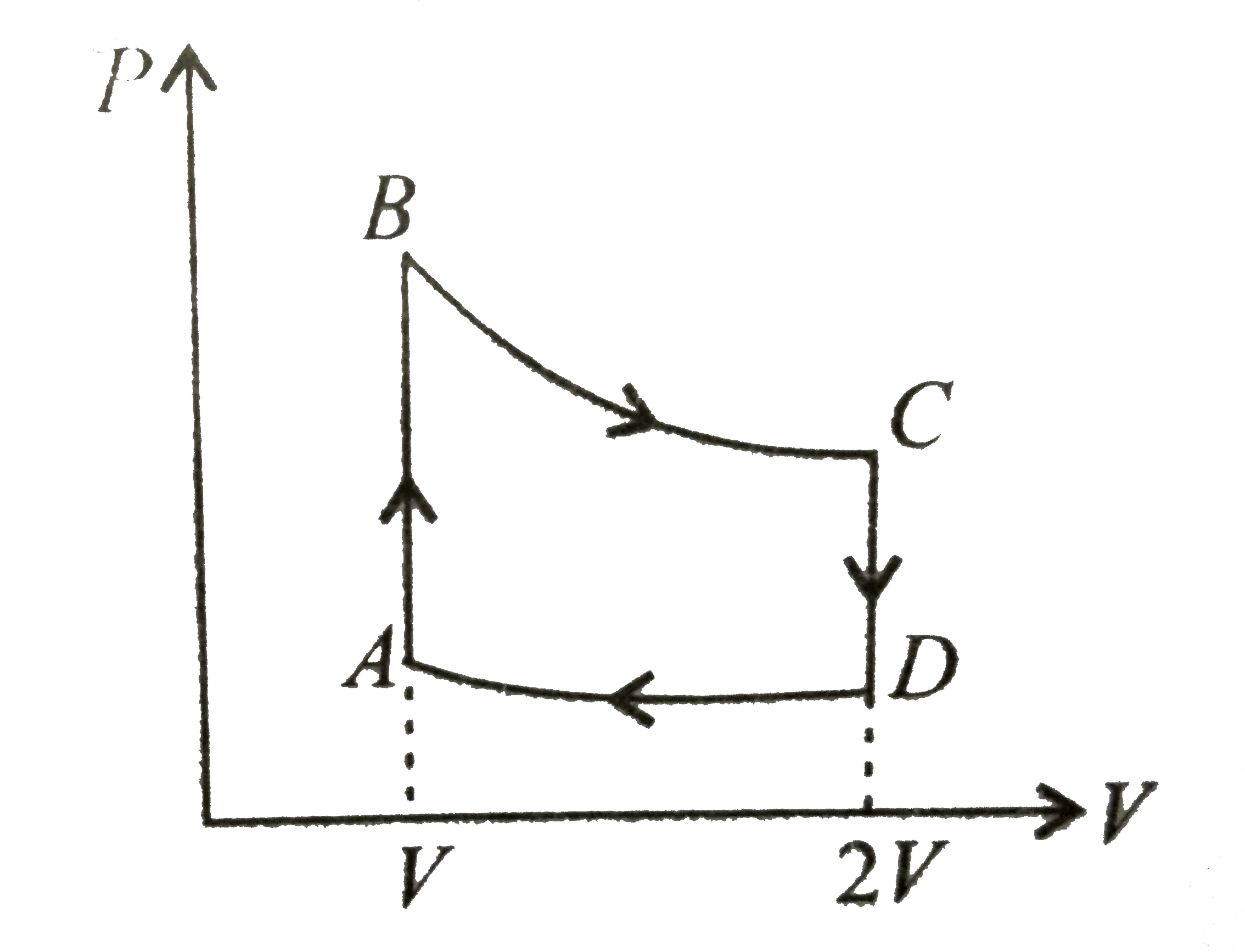
View SolutionThe cycle is shown in figure is made of one mole of perfect gas in a cylinder with a piston . The processes A to B and C to D are isochoric wheras process B to C and D to A are adiabatic, the work done in one cycle is (VA=VB=V,VC=VD=2Vand γ=5/3)
 04:55View Solution
04:55View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)09:00View SolutionA cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. CV=32R
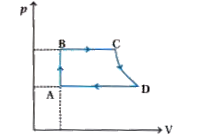
(a) A to B : constant volume
(b) B to C: constant pressure
(c) C to D: adiabatic
(d) D to A: constant pressure13:37View SolutionA cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure. A to B volume constant, B to C adiabatic, C to D volume constant and D to A adiabatic " "V_(C)=V_(D)=2V_(A) = 2V_(B) (a) In which part of the cycle heat is supplied to the engine form outside? (b) In which part of the cycle heat is being given to the surrounding by the engine ? (c ) What is the work done by the engine in one cycle ? Write your answer in term of p_(A),p_(B),V_(A) ? (d) What is the efficiency of the engine ? " "(gamma=(5)/(3) for the gas ) , (C_(V)= (3)/(2)R for one mole )
08:28View SolutionThe cycle in the figure followed by an engine made of an ideal gas in ca cylinder with a piston, the heat exchanged by the engine with the surroundings for adiabatic section AB of cycle is (C_(V)=(3)/(2)R)
04:57View SolutionA cycle followed an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in figure The heat exchanged by the engine with the surroundings at constant volume is (Take C_(V)=(3)/(2)R)
View Solution
