One mole of a monatomic ideal gas is taken through the cycle shown in the figure: adiabatic expansion
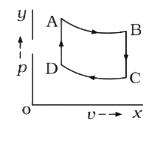
cooling at constant volume
adiabatic compression heating at constant volume.
The pressure and temperature at etc. etc. are denoted etc. respectively. Given that
and
Calculate the following quantities.
The heat lost by the gas in process (in J)
The correct Answer is:
Heat lost by the gas in process
From gas laws (at constant volume)
or
Similar Questions
One mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The work done by the gas in process A→B (in J)View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
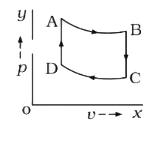
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]View Solution
Knowledge Check
- Question 1 - Select One
One mole of a monatomic ideal gas is taken through the cycle shown in figure
The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option. AThe work done by the gas in the process A→B is 1869.75JBThe heat lost by the gas sin the process B→C is -5297.25JCTemperature TD is 500KDWork done from B→C is 40J - Question 2 - Select One
One mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC
[Assume(23)0.4=0.85 and R=253JK−1mol−1]
The temperature at B isA350KB1175KC850KD577K - Question 3 - Select One
Two moles of a diatomic gas are carried trhough the cycle ABCDA as shown in figure. The segment AB represents an isothermal expansion, the segment BC an adiabatic expansion. The pressure and temperature at A are 5 atm and 600K respectively. The volume at B is twice that at A. The pressure at D is 1 atm.
What is the pressure at B?A2.5 atmB3 atmC3.5 atmD2 atm
One mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
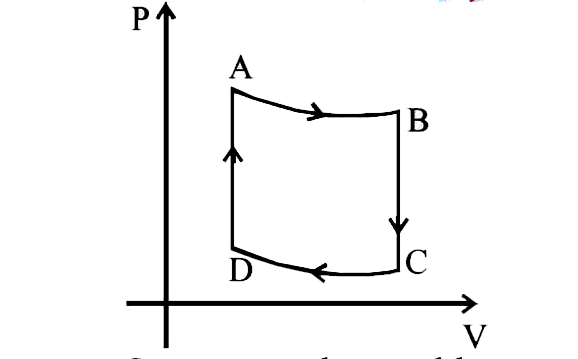
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−KView SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionIn an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
View Solution