A cyclotron is operated at an oscillator frequency of 12 MHz and has a dee radius R 50 cm. What is the magnitude of the magnetic field needed for a proton to be accelerated in the cyclotron?
0.78 T
0.65 T
0.39 T
0.12 T
The correct Answer is:A
To find the magnitude of the magnetic field needed for a proton to be accelerated in a cyclotron, we can use the formula:
B=2πmfq
where:
- B is the magnetic field,
- m is the mass of the proton,
- f is the frequency of oscillation,
- q is the charge of the proton.
1. Identify the given values:
- Frequency f=12MHz=12×106Hz
- Radius R=50cm=0.5m (not needed for this calculation)
- Mass of the proton mp=1.672×10−27kg
- Charge of the proton q=1.602×10−19C
2. Substitute the values into the formula:
B=2π(1.672×10−27kg)(12×106Hz)1.602×10−19C
3. Calculate the numerator:
- First, calculate 2π:
2π≈6.2832
- Now calculate the product:
6.2832×1.672×10−27×12×106
- This gives:
≈1.267×10−19kg⋅Hz
4. Calculate the magnetic field B:
B=1.267×10−191.602×10−19≈0.79T
5. Final result:
- The magnitude of the magnetic field needed for a proton to be accelerated in the cyclotron is approximately:
B≈0.79Tesla
- B is the magnetic field,
- m is the mass of the proton,
- f is the frequency of oscillation,
- q is the charge of the proton.
- Frequency f=12MHz=12×106Hz
- Radius R=50cm=0.5m (not needed for this calculation)
- Mass of the proton mp=1.672×10−27kg
- Charge of the proton q=1.602×10−19C
B=2π(1.672×10−27kg)(12×106Hz)1.602×10−19C
- First, calculate 2π:
2π≈6.2832
- Now calculate the product:
6.2832×1.672×10−27×12×106
- This gives:
≈1.267×10−19kg⋅Hz
B=1.267×10−191.602×10−19≈0.79T
- The magnitude of the magnetic field needed for a proton to be accelerated in the cyclotron is approximately:
B≈0.79Tesla
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionA circular coil of wire consisting of 100 turns, each of radius 8.0cm carries a current of 0.40A.
What is the magnitude of the magnetic field →B at the center of the coil?View SolutionA solenoid of length 0⋅5m has a radius of 1cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid?
View SolutionAn AC rms voltage of 2V having a frequency of 50 KHz is applied to a condenser of capacity of 10μF. The maximum value of the magnetic field between the plates of the condenser if the radius of plate is 10cm is
View SolutionA circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field (→B) at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of loop is R. What is the magnitude of magnetic field induciton at the centre of the loop?
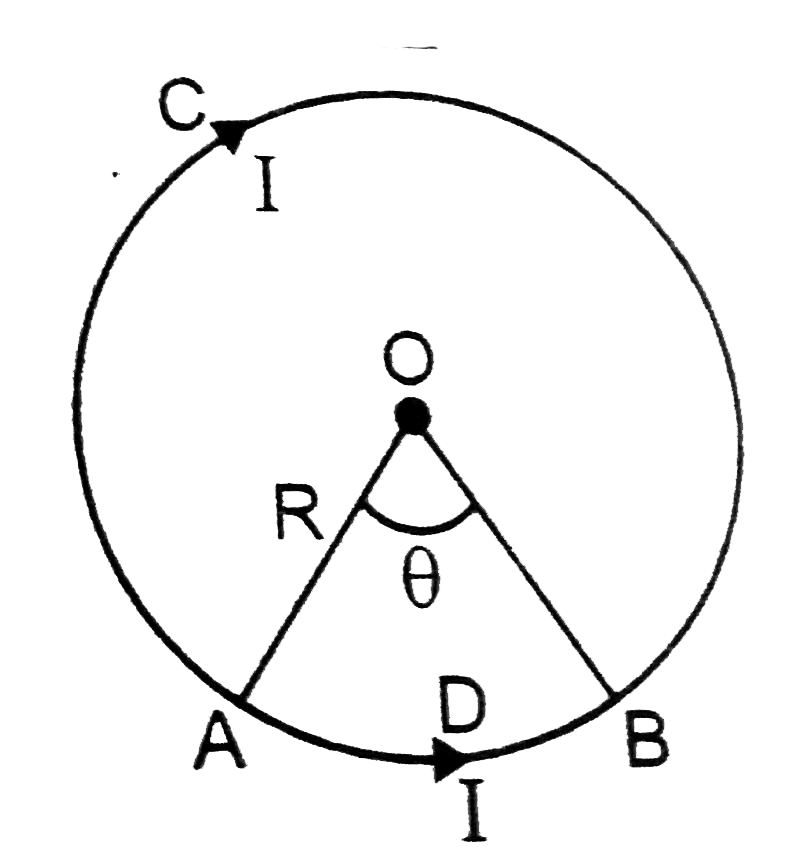 View Solution
View SolutionIf the cyclotron oscillator frequency is 16 MHz, then what should be the operating magnetic field for accelerating the proton of mass 1.67×10−27kg?
View SolutionA cyclotron's oscillator frequency is 10MHz. What should be the operating magnetic field fro accelerating protons? If the radius of its dees is 60cm, what is the kinetic energy (in MeV) of the proton beam produced by the acceleration?
(e−1.60×10−19C,mp=1.67×10−27kg,1MeV=1.6×10−13J)View SolutionA cyclotron is used to obtain 2 Me V protons. If the frequency is 5MHz and potential is 20kV. The magnetic field necessary for resonance is
View SolutionAn insect trapped in a circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100s.What is the magnitude of the centripetal acceleration.
View Solution

