A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment →M
is non-zero and points in the z-direction by symmetry
points along the axis of the toroid (→M=mˆϕ)
is zero, otherwise there would be a field falling as 1r3 at large distances outside the toroid
is pointing radially outwards.
The correct Answer is:A
To find the magnetic moment →M of a toroid with n turns, mean radius R, cross-sectional radius a, and carrying current I, we can follow these steps:
1. Understanding the Geometry of the Toroid:
- A toroid is essentially a circular ring with wire wound around it. The mean radius R is the distance from the center of the toroid to the center of the wire coil, while a is the radius of the cross-section of the toroid.
2. Magnetic Moment Formula:
- The magnetic moment →M of a current-carrying loop is given by the formula:
→M=n⋅I⋅A
where n is the number of turns, I is the current, and A is the area of the loop.
3. Calculating the Area A:
- For a toroid, the area A can be approximated as the area of the circular cross-section of the toroid:
A=πa2
- Here, a is the radius of the cross-section.
4. Substituting the Area into the Magnetic Moment Formula:
- Now substituting the expression for area A into the magnetic moment formula:
→M=n⋅I⋅πa2
5. Direction of the Magnetic Moment:
- The direction of the magnetic moment →M is along the axis of the toroid, following the right-hand rule.
6. Conclusion:
- Therefore, the magnetic moment of the toroid is given by:
→M=n⋅I⋅πa2
- It is important to note that the magnetic field is confined within the toroid, and outside the toroid, the magnetic field is zero.
Final Answer:
The magnetic moment →M of the toroid is:
→M=n⋅I⋅πa2
- A toroid is essentially a circular ring with wire wound around it. The mean radius R is the distance from the center of the toroid to the center of the wire coil, while a is the radius of the cross-section of the toroid.
- The magnetic moment →M of a current-carrying loop is given by the formula:
→M=n⋅I⋅A
where n is the number of turns, I is the current, and A is the area of the loop.
- For a toroid, the area A can be approximated as the area of the circular cross-section of the toroid:
A=πa2
- Here, a is the radius of the cross-section.
- Now substituting the expression for area A into the magnetic moment formula:
→M=n⋅I⋅πa2
- The direction of the magnetic moment →M is along the axis of the toroid, following the right-hand rule.
- Therefore, the magnetic moment of the toroid is given by:
→M=n⋅I⋅πa2
- It is important to note that the magnetic field is confined within the toroid, and outside the toroid, the magnetic field is zero.
The magnetic moment →M of the toroid is:
→M=n⋅I⋅πa2
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSERTION AND REASON
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - Magnetism And Gauss'S Law
2 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - HIGHER ORDER THINKING SKILLS (HOTS)
8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
Similar Questions
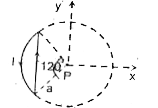
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA circular coil of radius 10cmand100 turns carries a current 1A. What is the magnetic moment of the coil?
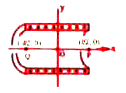
View SolutionA solenoid of length 'l' has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'P'(only axial component).
View Solution
