A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
For platform
x=Acosωt
v=dxdt=−Aωsinωt
a=dvdt=−ω2Acosωt
Maximum acceleration of platform
amax=ω2A.
Friction force acting on cylinder provides torque
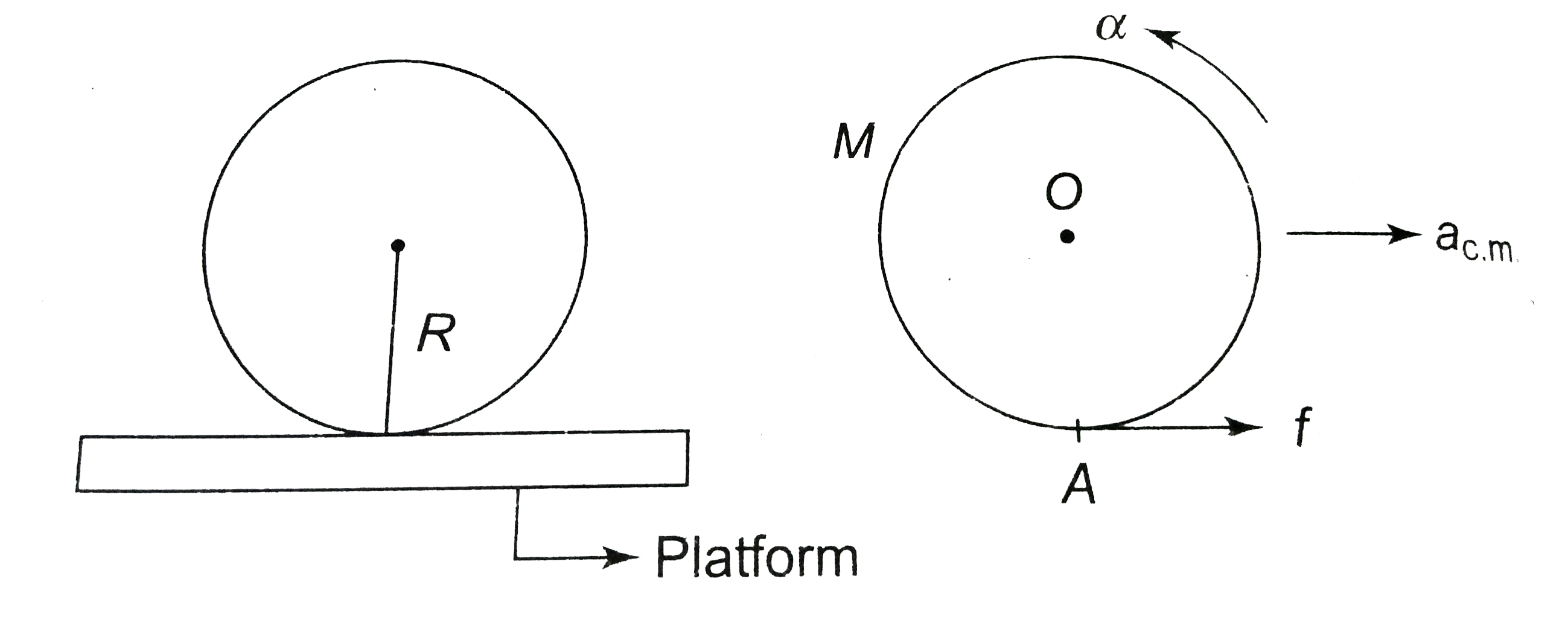
f=Mac.m.⇒ac.m=fM
f×R=I0α=12MR2α
α=2fMR
aA=ac.m.+Rα=fM+2fM=3fM
As there is no slipping between cylinder and platform, relative accelertion at point of contact should be zero, i.e.
aA=amax
3fM=ω2A⇒f=Mω2A3
Maximum torque by friction
τmax=fR=Mω2AR3
Topper's Solved these Questions
Similar Questions
A cylinder of mass M and radius R is resting on a horizontal paltform (which is parallel to the x-y plane) with its exis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acitng on the cylinder during its motion is ..................
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
A0.2N−mB2.0N−mC5.0N−mD10.0N−m - Question 2 - Select One
A cylinder of mass M, radius R is kept on a rough horizontal plane at one extreme end of the platfonn at t = 0. Axis of the cylinder is parallel to z-axis. The platform is oscillating in the xy-plane and its displacement from origin is represented by x = 4 cos(2πt) metres. There is no slipping between the cylinder and the platfonn. Find the acceleration of the centre of mass of cylinder at t =16s
(##TRG_PHY_MCQ_XII_C04_E04_001_Q01.png" width="80%">A−53π2B−23π2C−83π2D−43π2 - Question 3 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionThe M.I. of a hollow cylinder of mass M, radius R and length L about a tangential axis parallel to the length will be:
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View Solution

