A cylinder of mass m is kept on the edge of a plank of mass 2m and length 12m, which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is 0.1. The cylinder is given an impulse, which imparts it a velocity 7ms−1 but no angular velocity. Find the time after which the cylinder falls off the plank.
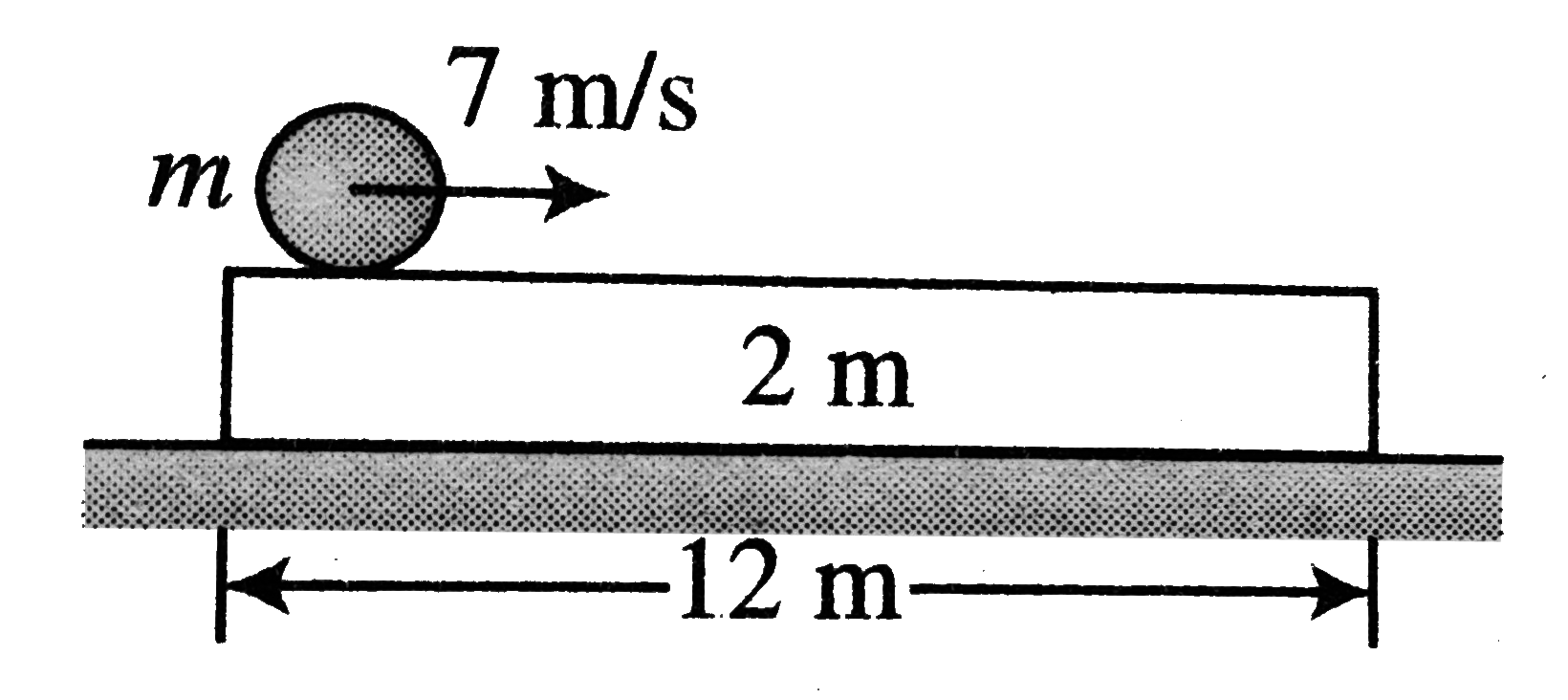

Initially the cylinder will slip on the plank, therefore kinetic energy friction will act between the cylinder and the plank.
ac=μmgm=−μg
aP=+μmg2m=+μ2
αC=(μmg)(R)(mR2/2)=+2μmgR
For pure rolling
vP=vC−Rωc
∴μ2t=v0−μ>−(R)(2μgR)(t)
∴t=v03.5μg=73.5×0.1×10=2s
∴sC−sP=v0t−12×μgt2−12(μg2)(t2)
=(7×2)−12(0.1)(10)(4)−12(0.1×102)(4)=11m
Also, vC−VP=(v0−μ>)−(μg2)(t)
=7−0.1×10×2−0.1×10×22=4m/s
Hence the remaining distance (12−11=1m) is travelled in a time
t'=1.04=0.25s
∴ total time =2+0.25=2.25s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid cylinder is kept on one edge of a plank of same mass and length 25 m placed on a smooth surface as shown in the figure. The coefficient of friction between the cylinder and the plank is 0.5. The plank is given a velocity of 20ms−1 towards right. Find the time (in S) after which plank any cylinder will separate. [g=10ms−2]

View SolutionA man of mass m1 stands at an edge A of a plank of mass m2 & length l which is kept on a smooth floor If man walks from A to the other edge B find displacement of plank.
View Solution
Knowledge Check
A cylinder of mass m is placed on the edge of a long plank of same mass kept on the smooth horizontal surface, where μ the is the coefficient of friction between cylinder and plank. The cylinder is given an impulse at t=0 which impacts it is velocity V0. find the time in which pure rolling starts.
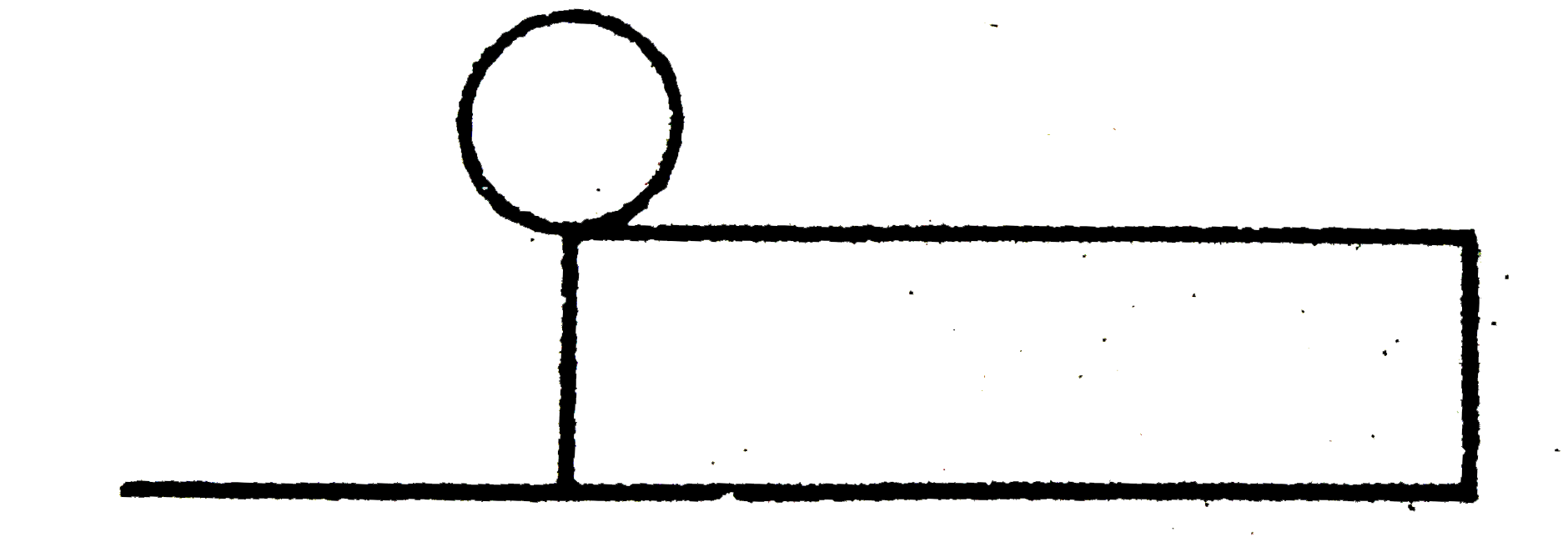 AV0/2μgBV0/4μgCV02√2μgDV0/4√2μg
AV0/2μgBV0/4μgCV02√2μgDV0/4√2μgA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
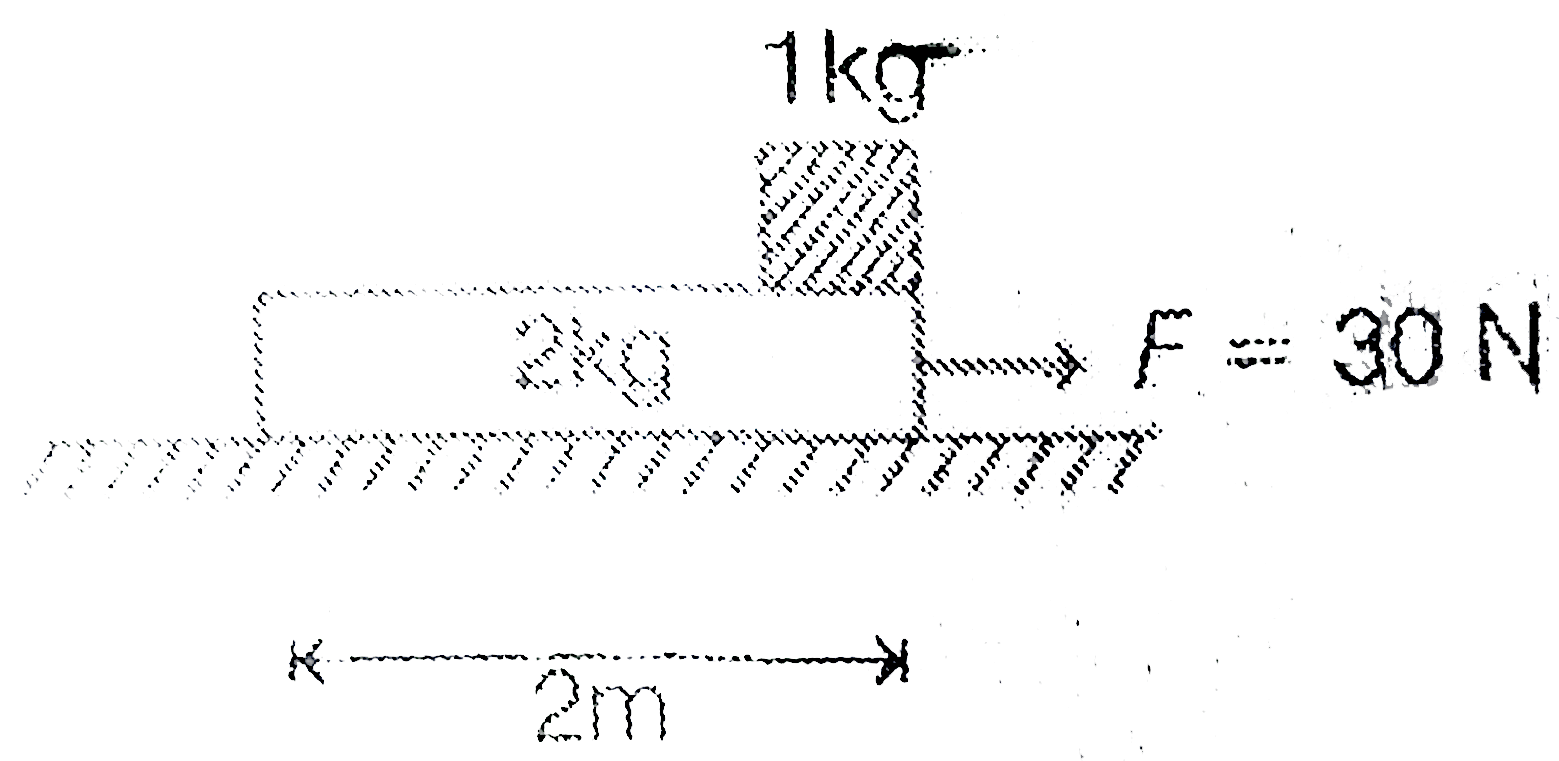 A0.89sB1.2sC0.62sD1.6s
A0.89sB1.2sC0.62sD1.6sA uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then
 Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of these
Afor pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is Ma/3Bthe maximum value of a, so that cyliner performs pure rolling is 3μgCThe acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a/3Dnone of these
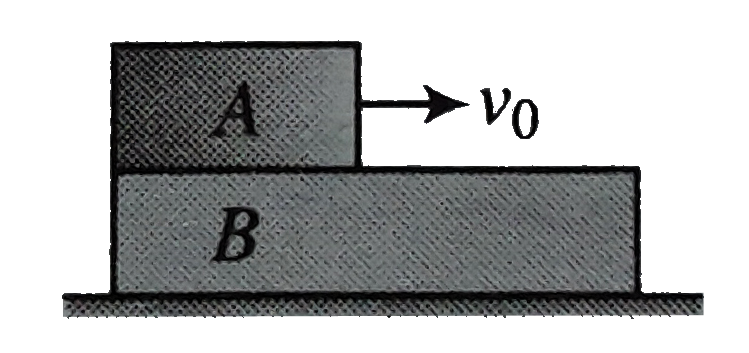
A block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA plank of length 20m and mass 1kg is kept on a horizontal smooth surface. A cylinder of mass 1lg is kept near one end of the plank. The coefficient of friction between the two surface is 0.5. The plank is suddenly given a velocity 20m/s towards left

Which of the following statements is correct?
View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :

View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
View Solution
