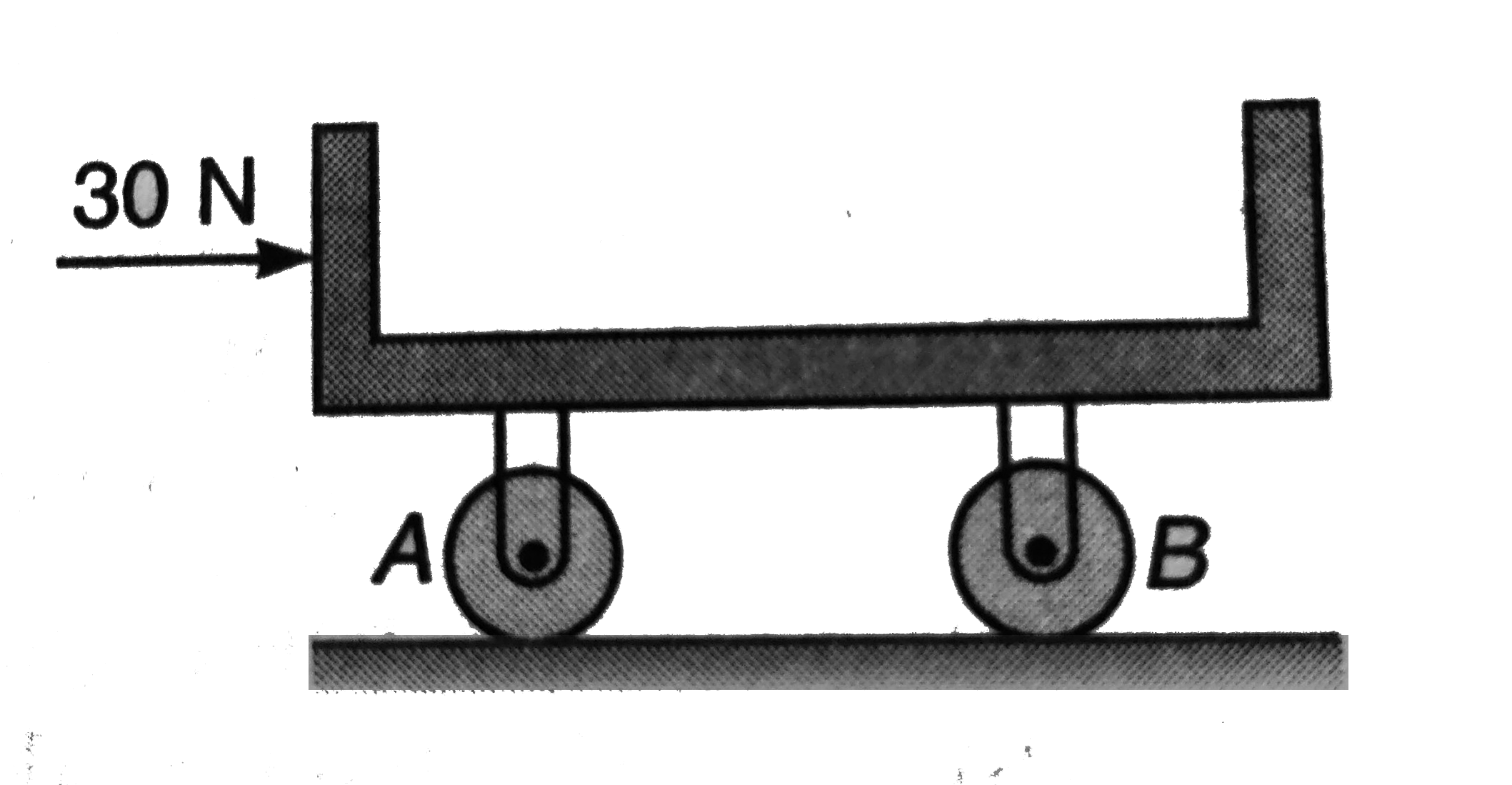
The 9 kg cradle is supported as shown by two uniform disks that roll without sliding at all surfaces of contact. The mass of each disk is m=6kg and the radius of each disk is r=80mm. Knowing that the system is initially at rest, determine the velocity of the cradle after it has moves 250 mm.
In rolling without sliding on a stationary ground, work done by friction is zero. Hence
work done by the applied force
= change in kinetic energy
∴(30)(0.25)=12×9×v2
+2[12×6×v2+12×12×6×r2×v2r2]
or 7.5=13.5v2
∴v=0.745m/s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Two uniform cylinders, each of mass m=10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine
the velocity of the centre of cylinder A after it has moved through 1.2 m &
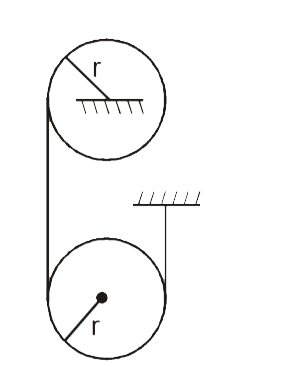
View SolutionTwo uniform cylinders, each of mass m=10 kg and radius r = 150 mm, are connected by a rough belt as shown. If the system is released from rest, determine
the tension in the portion of the belt connecting the two cylinders.
View Solution
Knowledge Check
A uniform disc of mass m and radius r rolls without slipping along a horizontal surface and ramp, as shown above. The disk has an initial velocity of υ . What is the maximum height h to which the center of mass of the disc rises ?
 Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22g
Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22gAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.A√2k3mB3x√k2mCx√3k2mDnone of theseA solid disk rotates in the horizontal plane at an angular velocity of 0.067rad/s with respect to an axis perpendicular to the disk at its center. The moment of inertia of the disk is 0.10kg.m2. From above, sand is dropped straight down onto this rotating disk, so that a thin uniform ring of sand is formed at a distance of 0.40 m from the axis. The sand in the ring has a mass of 0.50 kg. After all the sand is in place, what is the angular velocity of the disk?
A0.067rad/sB0.046rad/sC0.059rad/sD0.037rad/s
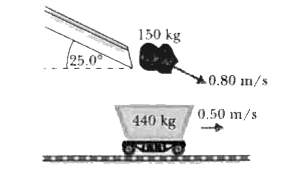
A mine car (mass = 440 kg) rolls at a speed of 0.50 m/s on a horizontal track, as the drawing shows. A 150 kg chunk of coal has a speed of 0.80 m/s when it leaves the chute. Determine the velocity of the car/coal system after the coal has come to rest in the car.
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
View SolutionIn the fig as shown a certain mass M is free to slide without friction on a horizontal table. This mass is connected by a light thread to a mass m that hangs over the edge of the table. The connecting thread passes over a frictionles pulley in the shape of a disk with radius R and mass mp. Calculate the velocity of the string after the hanging mass has fallen a distance h starting from test.

View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
View Solution
