A cylindrical capacitor conneced to a $d c$ voltage source $V$ touches the surface of water with its end (Fig) The sepration $d$ between the capacitors electrodes is substantially less than their mean radius. Find a height $h$ to which the water level in the gap will rise. The, capilary effects are to be negelected.

Video Solution

Text Solution

Verified by Experts

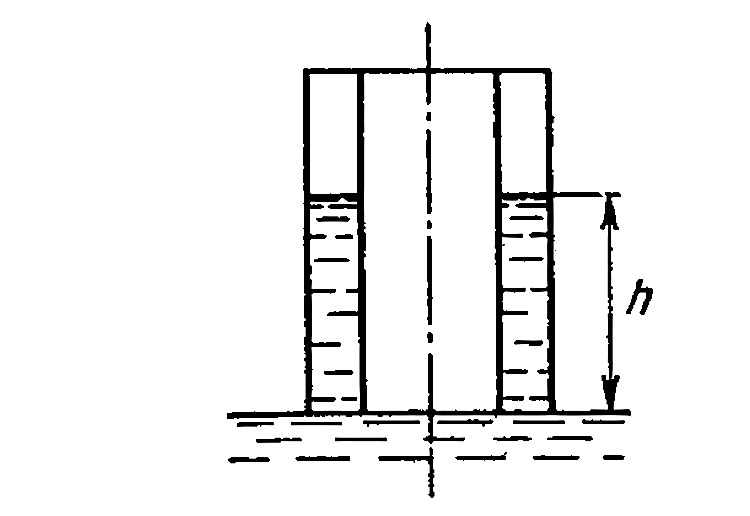
If $C_{0}$ is the inital capacitance of the condenser before water rises in it then
$U_{i} = \frac{1}{2} C_{0} V^{2}$ , where $C_{0} = \frac{ε_{0} 2 l π R}{d}$
( $R$ is the mean radius and $l$ is the length of the capacitor plates.)
Suppose the liquid rises to a height $h$ in it. Then the capacitance of the condenser is
$C = \frac{ε ε_{0} h 2 π R}{d} + \frac{ε (l - h) 2 π R}{d} = \frac{ε_{0} 2 π R}{d} (l + (ε - 1) h)$
and energy of the capacitor and the liquid (inculding both gravitational and electrostatic condtributions) is epsilon $\frac{1}{2} \frac{ε_{0} 2 π R}{d} (l + (ε - 1) h) V^{2} + ρ g (2 π R h d) \frac{h}{2}$
If the capacitor were not connected to a battery this energy would have to be minimized. But the capacitor is connected to the battery and in effect the potential energy of the capacitor and the liquid increases by
$δ h (\frac{ε_{0} 2 π R}{2 d} (ε - 1) V^{2} + ρ g (2 π R d) h)$
and that of the cell diminishes by the quantity $A_{c e l l}$ which is the product of charge flown and $V$
$δ h \frac{ε_{0} (2 π R)}{d} (ε - 1) V^{2}$
In equilbrium, the two must balance, so
$ρ g d h = \frac{ε_{0} (ε - 1) V^{2}}{2 d}$
Hence $h = \frac{ε_{0} (ε - 1) V^{2}}{2 ρ g d^{2}}$

Two identical capacitors are connected in series with a source of constant voltage $V$ . If $Q$ is the charge on one of the capacitors, the capacitance of each capacitor is :
A $Q / 2 V$
B $Q / V$
C $2 Q / V$
DNone of these
Water pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
A $\frac{Q}{π r h}$
B $\frac{Q}{π r^{2}}$
C $\frac{Q}{2 π r^{2}}$
D $\frac{Q}{π r^{2} h}$