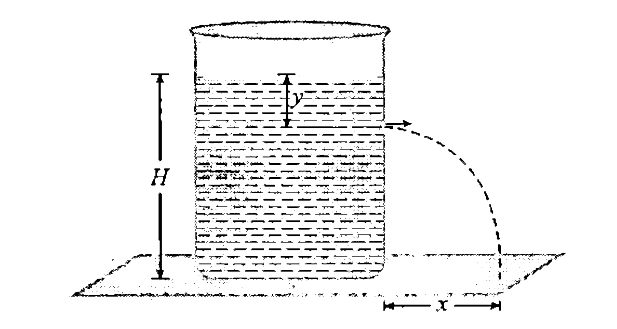
A cylindrical container has mass M and height H. the centre of mass of the empty container is at height H2 from the base. A liquid, when completley filled in the container, has mass M2 this liquid is poured in the empty contaienr.
(a) How does the centre of mass of the system (container+liquid) move as the height (x) of liquid column changes from zero to H? Explain your answer qualitatively. Draw a graph showing the variation of height of centre of mass of the system (xcm) with x.
(b) Find the height of liquid column x for which the centre of mass is at its lowest position.

The correct Answer is:(a) The COM first falls attains a minimum height and then it rises to original height H2
(b) x=(√6−2)H
Topper's Solved these Questions
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionTwo lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v . Neglect mass of the container. In this case
View SolutionAn open cubical container of side 'H' is filled with a liquid up to height H4 . Mass of liquid inside container is 'm' (neglect atmospheric Pressure). When container is moved with maximum possible acceleration what will be the value of force applied by liquid on front wall parallel to plane of paper ?

View SolutionA cylindrical vessel of radius R=1m and height H=3m is filled with an ideal liquid up to a height of h=2 m. the contaienr with liquid is rotated about its central vertical axis such that the liquid just rises to the brim. Calculate the angular speed (omega) of the container.
View SolutionA liquid has been poured into a cylindrical vessel of mass M (the mass of the vessel bottom can be ighored) and height H. The linear density of the liquid, that is, the ratio of the mass of the liquid column to its height, is δ. What is the height x of the column of liquid at which the common center of gravity of the liquid plus the vessel is in the lowest position?
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionProve that the average pressure of a liquid (density p) on the walls of the container filled upto height h with liquid is 12hρg.
View SolutionA container contains an incompressible and non - viscous liquid of density rho and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
View Solutionএকটি পাত্রে d ঘনত্বের তরল h উচ্চতা পর্যন্ত আছে। যদি পাত্রটি স্থির থাকে, তবে পাত্রের দেয়ালে গড় চাপ হবে।
View SolutionA hemisphereical bowl of internal diameter 36cm contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3cm and height 6cm. How many bottles are required to empty.
View SolutionA hemisphereical bowl of internal diameter 36cm contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3cm and height 6cm. How many bottles are required to empty.
View SolutionA hemisphereical bowl of internal diameter 36cm contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3cm and height 6cm. How many bottles are required to empty.
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
View Solution
