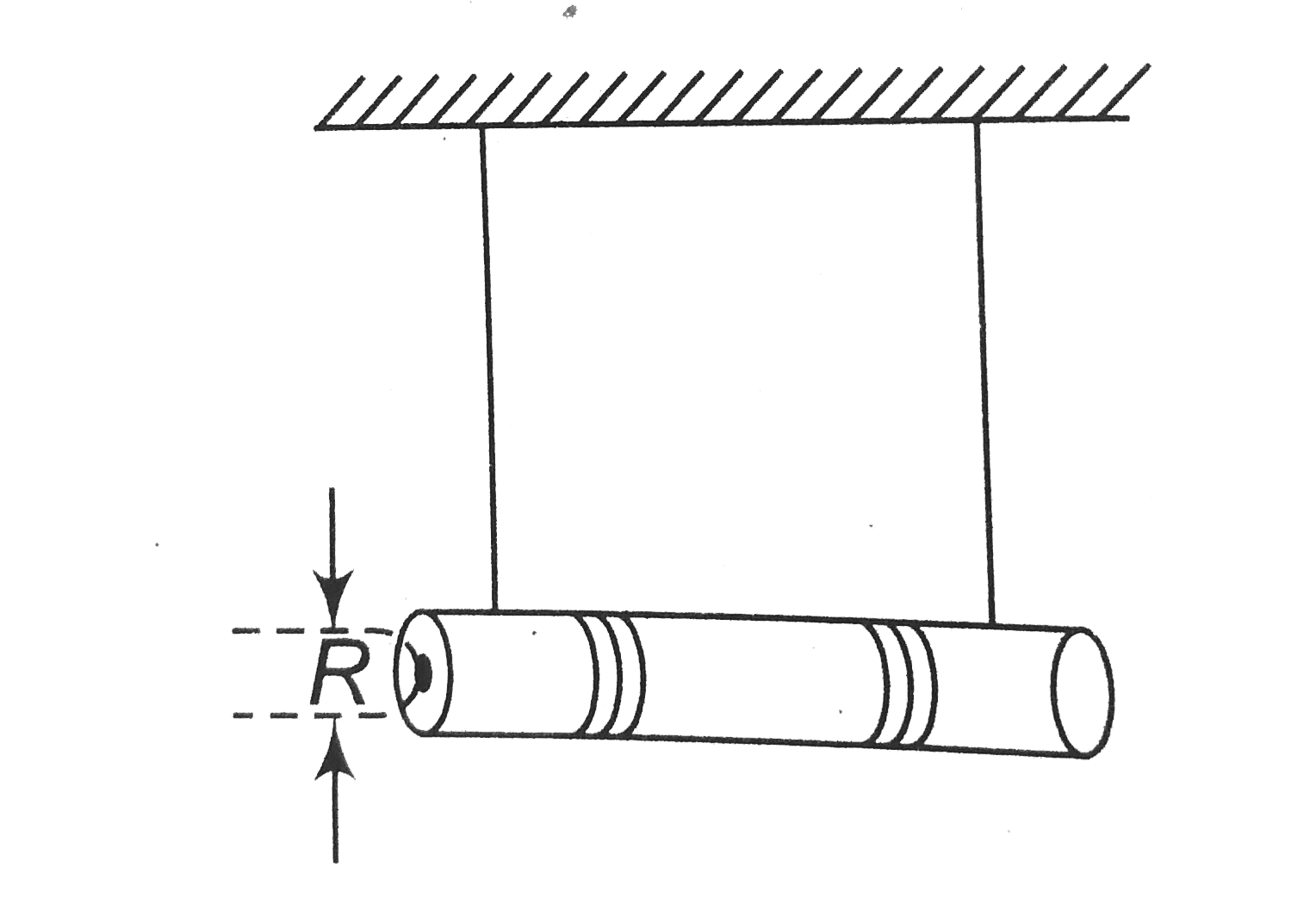
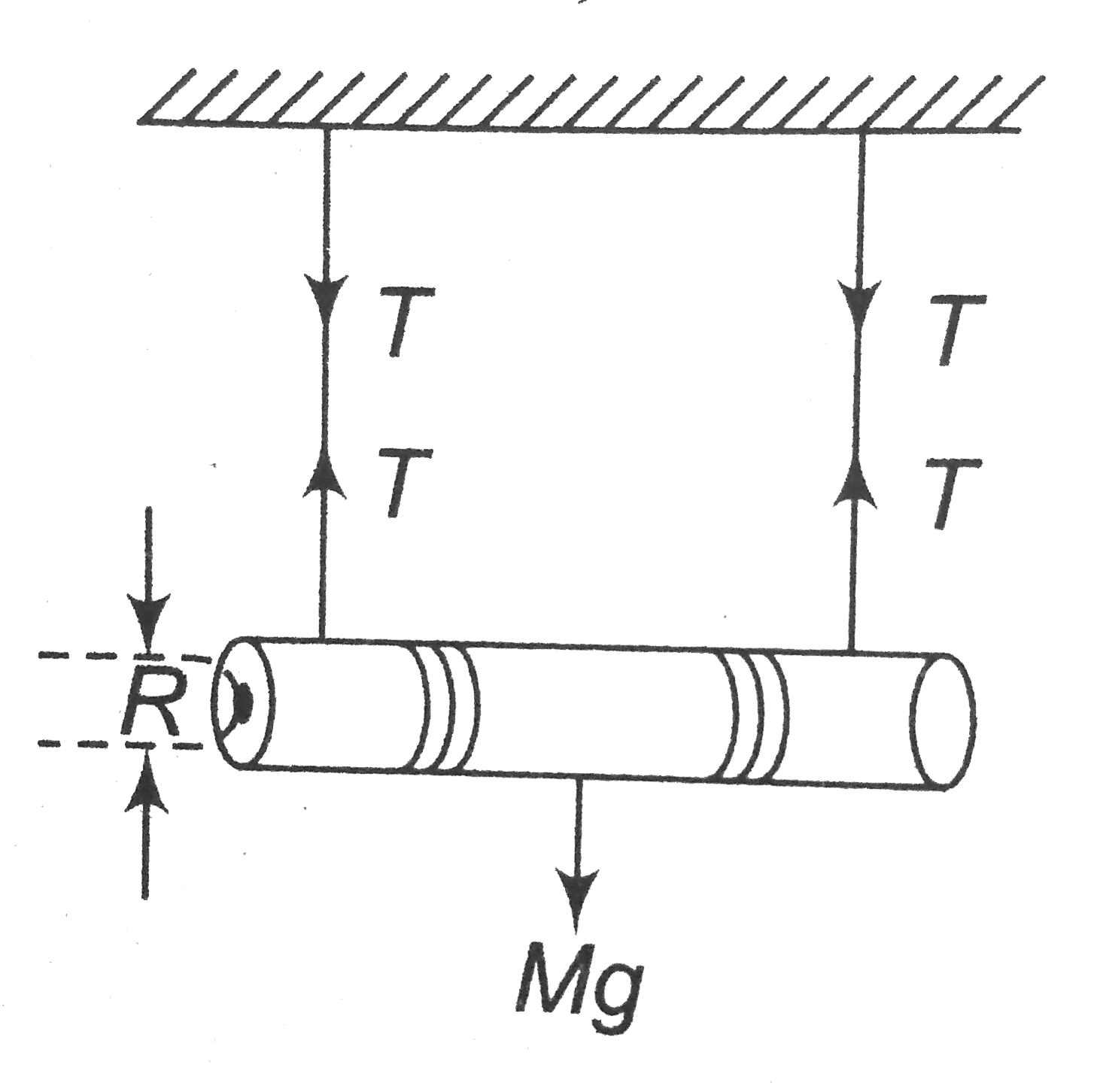
A cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
 .
.
g
g3
2g3
g2
The correct Answer is:C
( c) The cylinder rotating under gravity has both translational and rotational motions. Let v be the linear velocity of its centre of mass and ω its angular velocity about the axis of rotation , then in descending a distance h it will lose PE=Mgh while gain in
KE=(12Iω2+12Mv2)
Now Mgh=12Iω2+12Mv2
Here I=12MR2andv=Rω
So Mgh=12Mv2+12(12MR2)(v2R2)
v2=43gh
Differenting :
2vdvdt=43g(dhdt) or a=2g3.
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Assertion Reasoning
Explore 20 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:NEET Questions
Explore 59 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
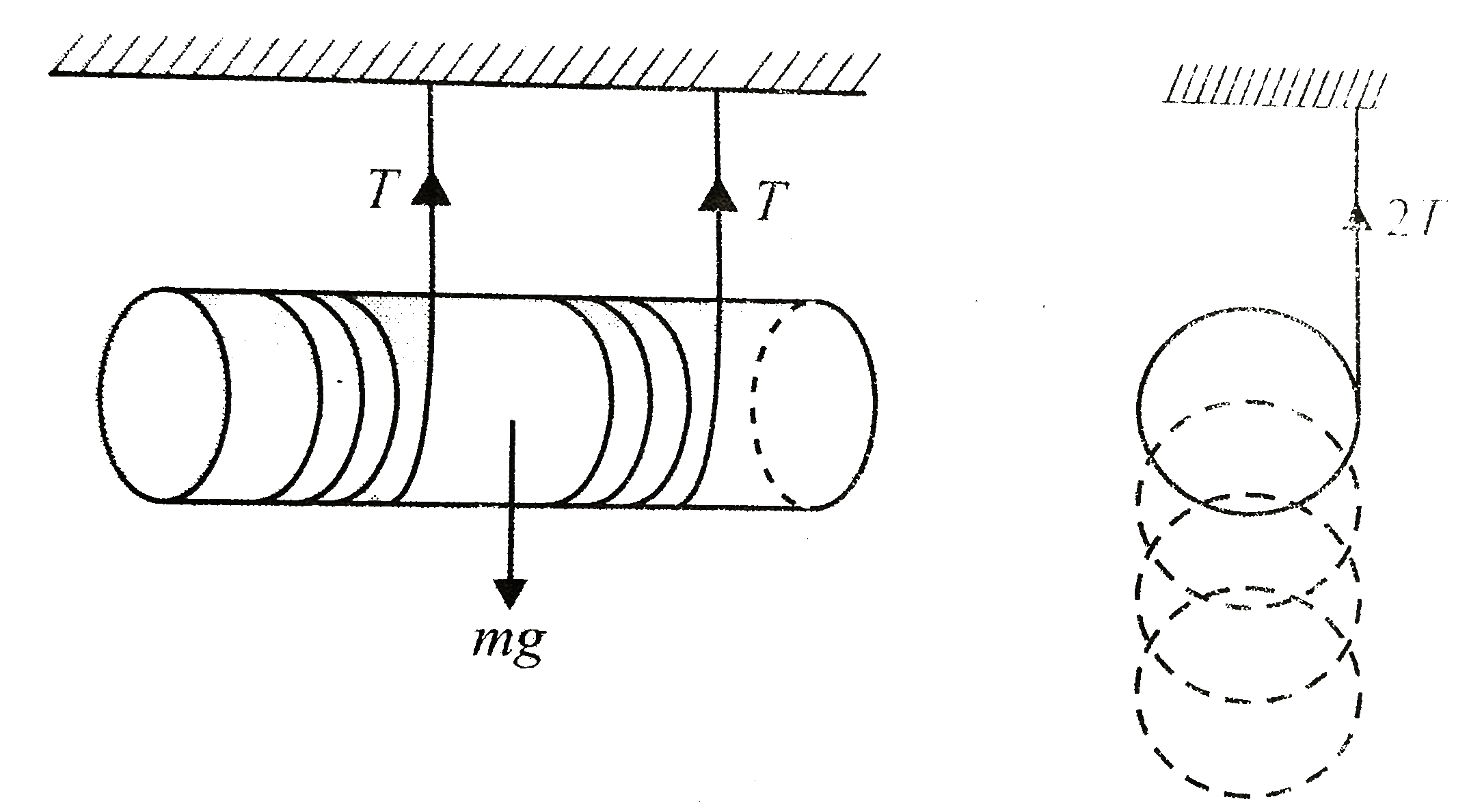
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution
Knowledge Check
A scylindrical rod of mass M, length L & radius R has cords wound around it , whose ends are attached to the ceioling .The rod is held borizontal and released .The liinear acceleration of the cylinder as it falls and tension in the cords is
Ag,Mg/2Bg/3,Mg/3C2g/3,Mg/6Dg/2,Mg/12A uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correctA solid cylinder of mass m=4kg and radius R=10cm has two ropes wrapped around it, one near each end. The cylinder is held horizontally by fixing the two free ends of he cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the tension along the strings.
A6.53NB5.23NC3.23ND4.43N
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
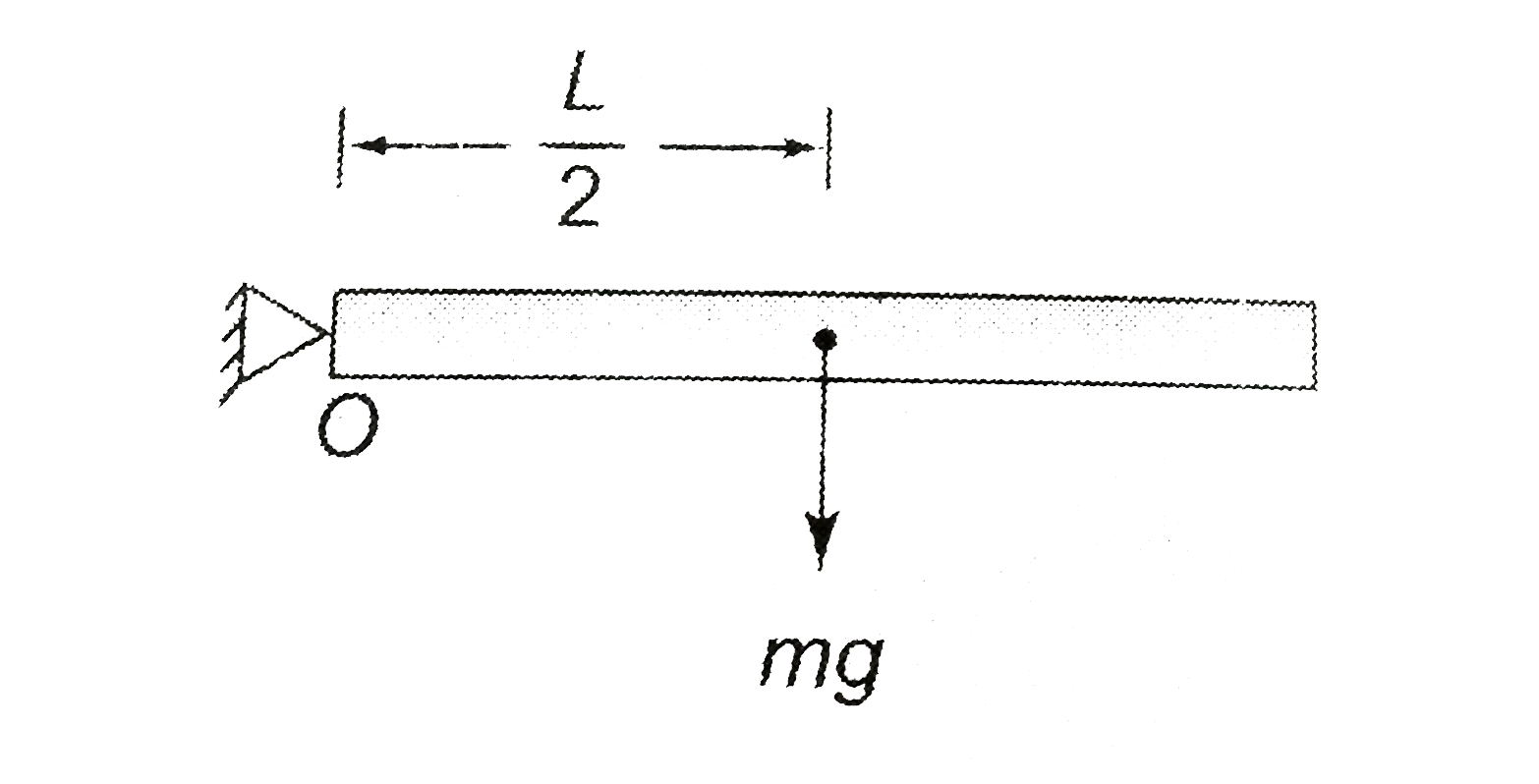
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View SolutionTwo blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.

View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View Solution