A cylindrical tank having cross-sectional area $A = 0.5 m^{2}$ is filled with two liquids of density $ρ_{1} = 900 k g m^{- 3}$ and $ρ_{2} = 600 k g m^{- 3}$ , to a height $h = 60 c m$ each as shown in the figure. A small hole having area $a = 5 c m^{2}$ is made in right vertical wall at a height $y = 20 c m$ from the bottom. A horizontal force $F$ is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids ( $a k e$ g = 10 ms^(-2)).

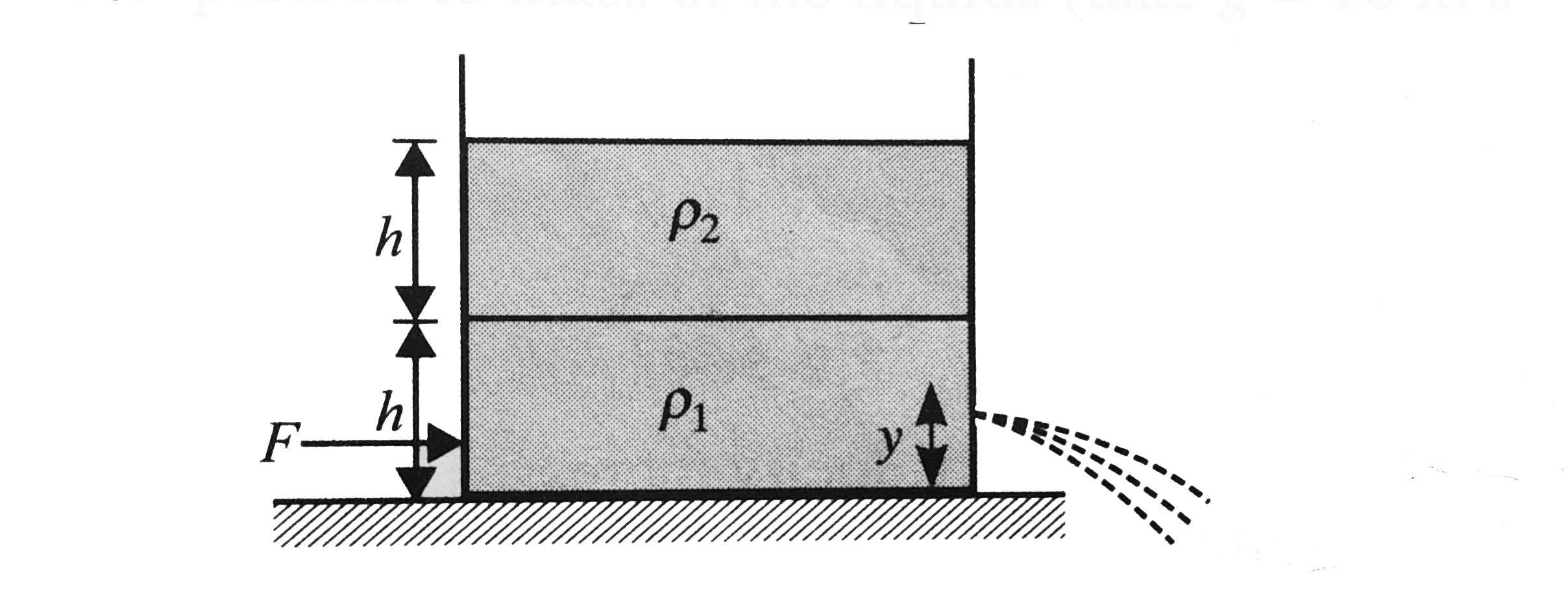
The velocity of efflux is

$10 m s^{- 1}$

$20 m s^{- 1}$

$4 m s^{- 1}$

$35 m s^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Since area of a hole is very small in comparison to base area $A$ of the cylinder, velocity of liquid inside the cylinder is negligible.
Let velocity of effux be $v$ and atmospheric pressure be $P_{0}$ . Consider two points $A$ (inside the cylinder) and $B$ (just outside the hole) in the same horizontal line as shown in the figure in question.
Pressure at $A, P_{A} = P_{0} + h ρ_{2} g + (h - y) ρ_{1} g$
Pressure at $B, P_{B} = P_{0}$
According to Bernoulli's theorem
Pressuure energy at $A =$ Pressure energy at $B +$ Kinetic energy at $B$
$∴ P_{A} = P_{B} + \frac{1}{2} ρ_{1} v^{2}$
$∴ v = 4 m s^{- 1}$

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Knowledge Check

A cylindrical tank having cross - sectional area $A = 0.5 m^{2}$ is filled with two liquids of density $ρ_{1} = 900 kg m^{- 3} and ρ_{2} = 600 kg m^{- 3}$ , to a height h $= 60 c m^{2}$ each.A small hole having area a=5 cm^2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take $g = 10 m s^{- 2}$ )

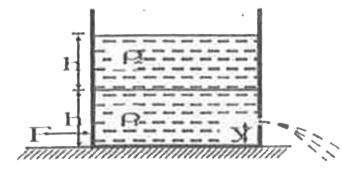
Horizontal force F to keep the cylinder in static equilibrium , if it is placed on a smooth horizontal thrust exerted by fluid jet . But that is equal to mass flowing per second $\times$ change in velocity of this mass
$∴ F = (a v ρ) (v - 0) = a ρ v^{2}$
or $F = 7.2 N$
A $7.2$ N
B $10 N$
C $15.5 N$
D $20.4$ N
A cylindrical tank having cross - sectional area $A = 0.5 m^{2}$ is filled with two liquids of density $ρ_{1} = 900 kg m^{- 3} and ρ_{2} = 600 kg m^{- 3}$ , to a height a $= 6 c m^{2}$ is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take $g = 10 m s^{- 2}$ )

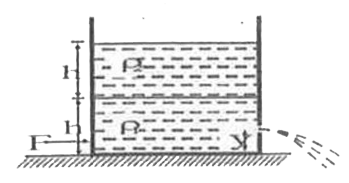
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is $0.01$
A0,40 N
B $5.4$ N , 52.2 N
C0 , 70 N
D0, $52.2$ N
A cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density $ρ_{1} = 600 k g / m^{3}$ and $ρ_{2} = 1200 k g / m^{3}$ as shown in the figure.
A small hole having cross sectional area $5 c m^{2}$ is made in right side vertical wall as shown. Take atmospheric pressure as $p_{0} = 10^{5} N / m^{2}, g = 10 m / s^{2}$ . For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as $1000 c m^{2}$ . Neglect the mass of the vessel.

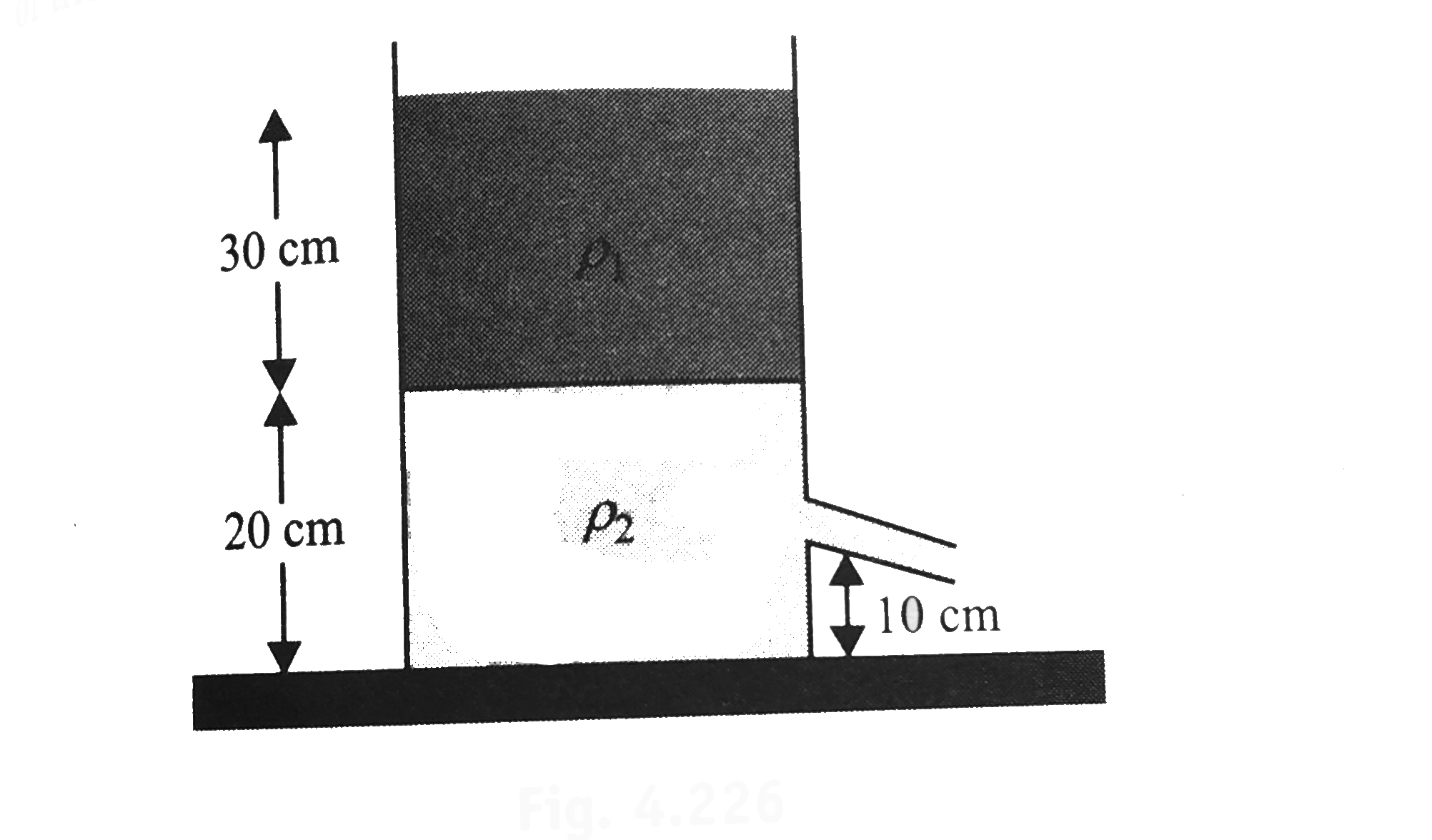AIf the surface on which the vessel is placed is smooth, then a rightward force of magnitude $3 N$ is to be applied on the vessel to maintain its static equilibrium.
BIf the surface on which the vessel is placed is smooth, then no force is needed to maintain its static equilibrium.
CIf the surface on which the vessel is placed is rough $(μ = 0.04)$ , then the minimum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is zero.
DIf the surface on which the vessel is placed is rough $(= 0.04)$ then the maximum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is $19.8 N$ .