A cylindrical wavefront spreads form a line source which is comparable to a long and narrow slit. The wavefront is at a distance d form source then th amplitude of wave is proportional to
1d
1d2
1d3
1d1/2
The correct Answer is:D
Step by step video, text & image solution for A cylindrical wavefront spreads form a line source which is comparable to a long and narrow slit. The wavefront is at a distance d form source then th amplitude of wave is proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If the amplitude of waves at a distance r from line source is A. The amplitude at a distance 4r will be
A2ABACA/2DA/4Statement I: In Young's double-slit experiment, the two slits are at distance d apart. Interference pattern is observed on a screen at distance D from the slits. At a point on the screen which is directly opposite to one of the slits, a dark fringe is observed. Then, the wavelength of wave is proportional to the squar of distance between two slits.
Statement II: For a dark fringe, intensity is zeroAStatement I is True, statement II is True, Statement II is a correct explanation for Statement I.BStatement I is Ture, Statement II is Ture, Statement II is NOT a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True.If A is the amplitude of the wave coming from a line source at a distance r, then :
AA∝rBA∝r−1/2CA∝r−2DA∝r1/2
The intensity of light at a distance r from the axis of a long cylindrical source is inversely proportional to r.
View SolutionThe intensity of light at a distance 'r' from the axis of a long cylindrical source is inversely proportional to 'r'
View SolutionAs a spherical wavefront propagates, the amplitude (a) of a spherical wavefront varies with the distance r of the source
View SolutionA line source emits a cylindrical expanding wave. Assuming the medium absorbs no energy find how the ampitude and intensity of wave depend on the distance from the source?
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
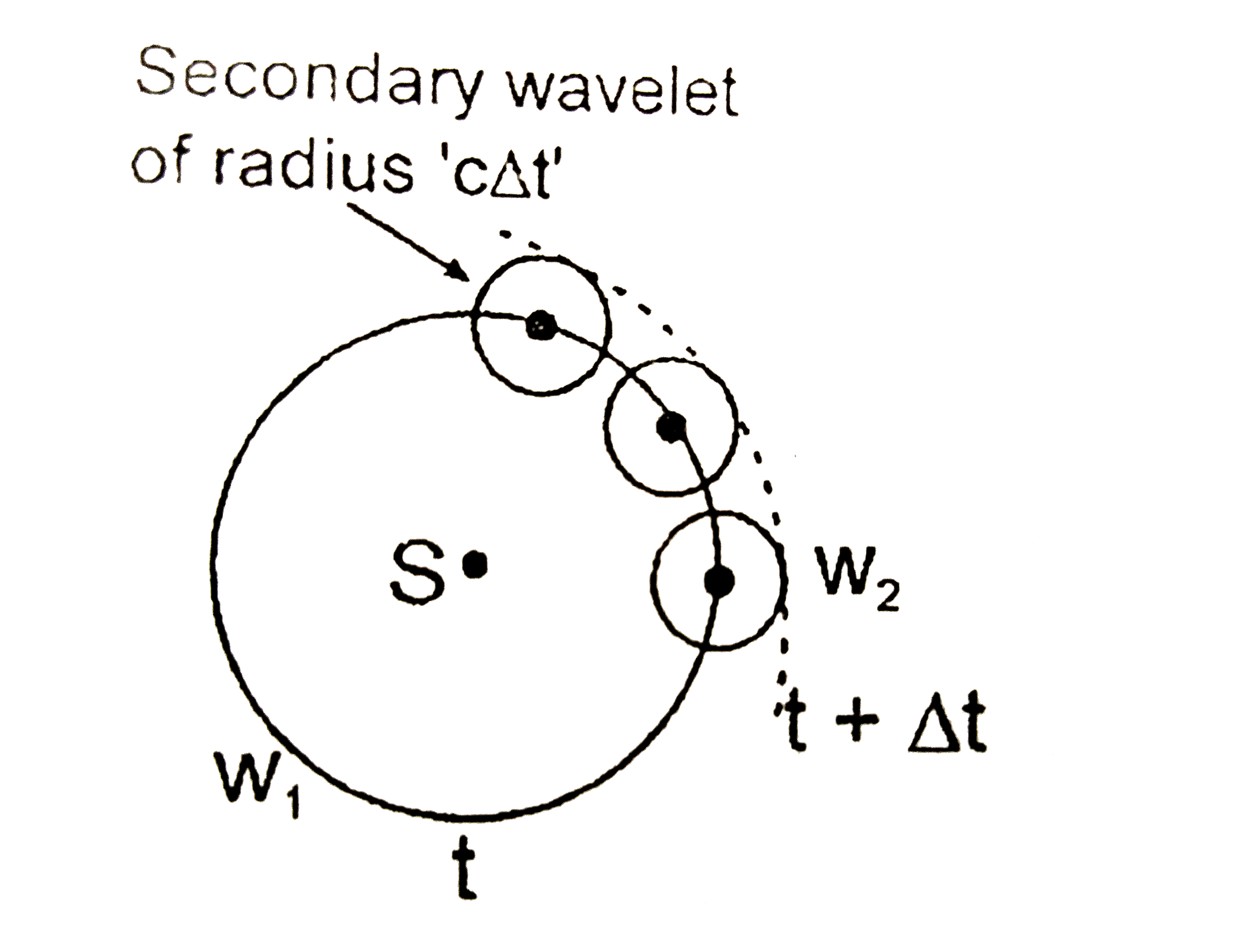
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View Solution
