A cylindrical wooden cork of mass 250 g and cross sectional area 10 cm2 is floating into a beaker filled with water, with an extra weight of 30 g attached to its bottom, as shown in the adjoining figure. If the cork Performs, S.H.M., determine its frequency. take,
Specific gravity of wood = 0.30
g=9.8m/s2
To solve the problem, we need to determine the frequency of the simple harmonic motion (SHM) of the floating cork with an attached weight. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
- The cork has a mass M=250g=0.25kg.
- An additional weight m=30g=0.03kg is attached to the cork.
- The total mass M+m=0.25kg+0.03kg=0.28kg.
- The cross-sectional area of the cork is A=10cm2=10×10−4m2=10−3m2.
Step 2: Calculate the Buoyant Force
- The buoyant force Fb acting on the cork is equal to the weight of the water displaced by the submerged part of the cork.
- The density of water ρw=1000kg/m3.
- The volume of water displaced when the cork is submerged to a depth h is V=A⋅h.
- The buoyant force can be expressed as:
Fb=ρw⋅V⋅g=ρw⋅A⋅h⋅g
Step 3: Set Up the Equilibrium Condition
- At equilibrium, the weight of the cork plus the attached mass equals the buoyant force:
(M+m)g=ρw⋅A⋅h⋅g
- Cancelling g from both sides, we have:
M+m=ρw⋅A⋅h
Step 4: Determine the Spring Constant
- The effective spring constant k for the system can be derived from the relationship between the buoyant force and the displacement x from the equilibrium position:
F=kx
- The spring constant k is given by:
k=ρw⋅A⋅g
Step 5: Calculate the Frequency of SHM
- The frequency f of SHM is given by:
f=12π√kmtotal
- Substituting k and mtotal:
f=12π√ρw⋅A⋅gM+m
Step 6: Plug in the Values
- Substitute the known values into the frequency formula:
f=12π√1000⋅10−4⋅9.80.28
- Simplifying:
f=12π√9800.28=12π√3500
- Calculating the square root:
√3500≈59.16
- Finally, calculate the frequency:
f≈59.166.283≈9.41Hz
Final Answer
The frequency of the simple harmonic motion of the cork is approximately 9.41Hz.
- The cork has a mass M=250g=0.25kg.
- An additional weight m=30g=0.03kg is attached to the cork.
- The total mass M+m=0.25kg+0.03kg=0.28kg.
- The cross-sectional area of the cork is A=10cm2=10×10−4m2=10−3m2.
- The buoyant force Fb acting on the cork is equal to the weight of the water displaced by the submerged part of the cork.
- The density of water ρw=1000kg/m3.
- The volume of water displaced when the cork is submerged to a depth h is V=A⋅h.
- The buoyant force can be expressed as:
Fb=ρw⋅V⋅g=ρw⋅A⋅h⋅g
- At equilibrium, the weight of the cork plus the attached mass equals the buoyant force:
(M+m)g=ρw⋅A⋅h⋅g
- Cancelling g from both sides, we have:
M+m=ρw⋅A⋅h
- The effective spring constant k for the system can be derived from the relationship between the buoyant force and the displacement x from the equilibrium position:
F=kx
- The spring constant k is given by:
k=ρw⋅A⋅g
- The frequency f of SHM is given by:
f=12π√kmtotal
- Substituting k and mtotal:
f=12π√ρw⋅A⋅gM+m
- Substitute the known values into the frequency formula:
f=12π√1000⋅10−4⋅9.80.28
- Simplifying:
f=12π√9800.28=12π√3500
- Calculating the square root:
√3500≈59.16
- Finally, calculate the frequency:
f≈59.166.283≈9.41Hz
The frequency of the simple harmonic motion of the cork is approximately 9.41Hz.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 2
20 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A cylinderical wooden block of cross-section 15.0 cm2 and mass 230g is floated over water with an extra weight of 50 g attached to its bottom. The cylider floats vertically. From the state of equilibrium, it is slightly depressed and released. If the specific gravity of wood is 0.30 and g=9.8ms−2 deduce the frequency of the block, A=15.0cm2=15×10−4m2
View SolutionIn the system shown in the adjoining figure, the acceleration of the 1 kg mass is m/s2. (take g=10m/s2)

View Solution
Knowledge Check
A cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.

The length of the cork cylinder inside the water in equilibrium isA6cmB4cmC8cmD3cmA cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.
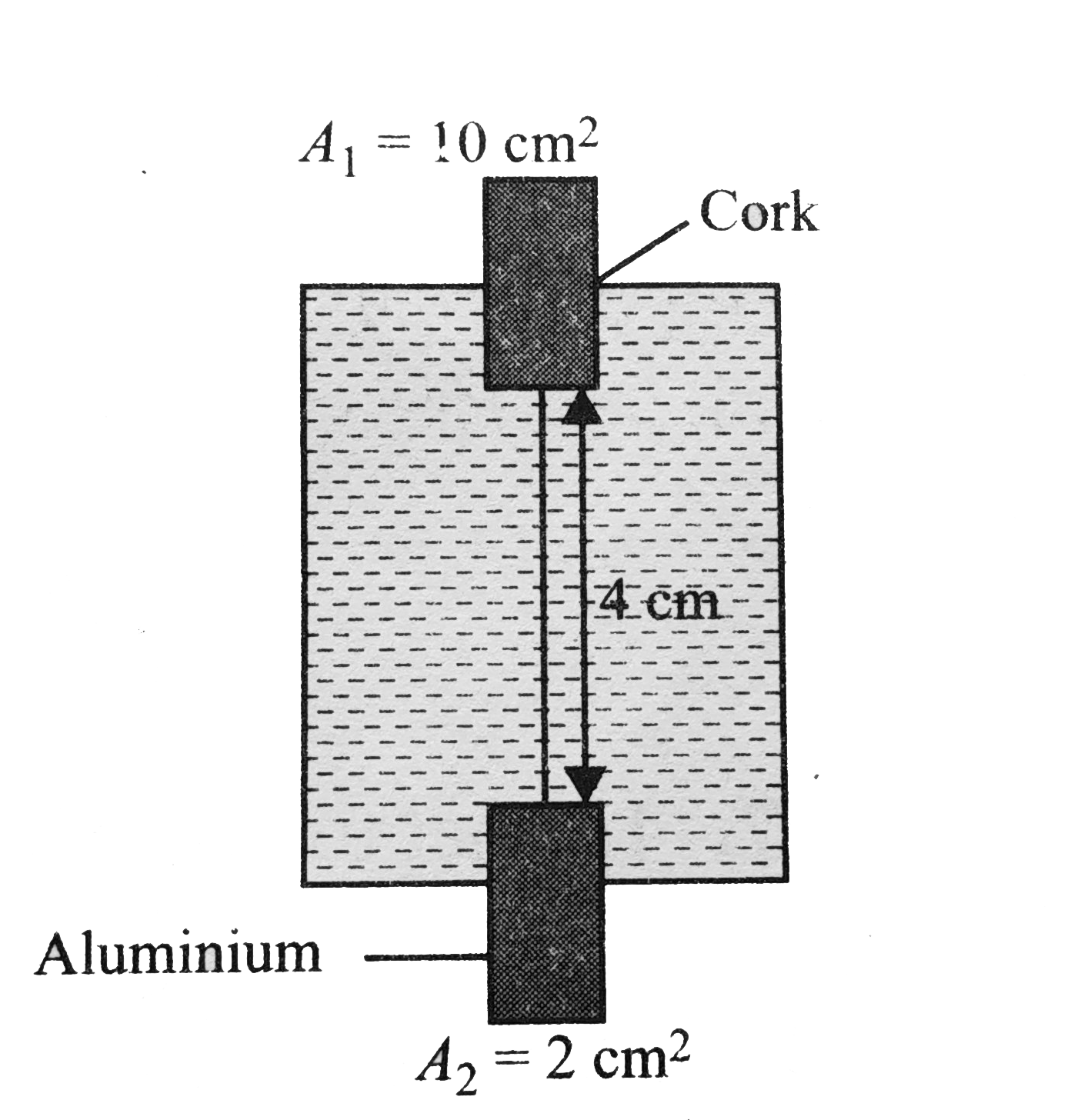
The tension in the string joining the cork and aluminium cylinder isA2NB1NC0.45ND0.6NA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
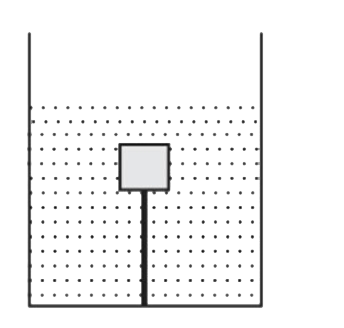 A2NB3NC5ND6N
A2NB3NC5ND6N
A wooden block of mass 20 gram and cross section 20 cm2 is floating on the surface of water. If it is slightly depressed and released from the equilibrium position, then calculate the frequency of oscillation of the block if specific gravity of wood is 0.28.
View SolutionA wooden cylinder of mass 20 g and area of cross-section 1cm2 , having a piece of lead of mass 60g attached to its bottom, floats in water. The cylinder is depressed and then released. The frequency of oscillation is NπS−1. Find the value of N. [Neglect the volume of water displaced by the lead piece, take g=9.8m/s2,density of water ρw=1gcm−3 ]
View SolutionThe weight of a body is 50 N. What is its mass? (g=9.8m/s2)
View SolutionWrite down the weight of a 50 kg mass on the earth. (g=9.8m/s2)
View SolutionA wooden cylinder of mass 20 g and area of cross-section 1cm2 , having a piece of lead of mass 60g attached to its bottom, floats in water. The cylinder is depressed and then released. The frequency of oscillation is NπS−1. Find the value of N. [Neglect the volume of water displaced by the lead piece, take g=9.8m/s2,density of water ρw=1gcm−3 ]
View Solution
