Calculate the time period and frequency of oscillation if the maximum velocity of a particle executing simple harmonic motion is 6 m/s and amplitude is 5 mm.
To solve the problem of calculating the time period and frequency of oscillation for a particle executing simple harmonic motion (SHM) with a maximum velocity of 6 m/s and an amplitude of 5 mm, we can follow these steps:
Step 1: Understand the relationship between maximum velocity, amplitude, and angular frequency
The maximum velocity vmax of a particle in SHM is given by the formula:
vmax=Aω
where:
- A is the amplitude,
- ω is the angular frequency.
Step 2: Convert amplitude to meters
The amplitude is given as 5 mm. We need to convert this to meters:
A=5mm=5×10−3m=0.005m
Step 3: Rearrange the formula to find angular frequency
From the formula vmax=Aω, we can solve for ω:
ω=vmaxA
Step 4: Substitute the known values
Now, substituting the values of vmax=6m/s and A=0.005m:
ω=6m/s0.005m=1200rad/s
Step 5: Calculate the time period
The time period T is related to angular frequency ω by the formula:
T=2πω
Substituting the value of ω:
T=2π1200≈6.28321200≈0.00524s
Step 6: Calculate the frequency
The frequency f is the reciprocal of the time period:
f=1T
Substituting the value of T:
f=10.00524≈191.0Hz
Final Answers
- Time Period T≈0.00524s
- Frequency f≈191.0Hz
---
The maximum velocity vmax of a particle in SHM is given by the formula:
vmax=Aω
where:
- A is the amplitude,
- ω is the angular frequency.
The amplitude is given as 5 mm. We need to convert this to meters:
A=5mm=5×10−3m=0.005m
From the formula vmax=Aω, we can solve for ω:
ω=vmaxA
Now, substituting the values of vmax=6m/s and A=0.005m:
ω=6m/s0.005m=1200rad/s
The time period T is related to angular frequency ω by the formula:
T=2πω
Substituting the value of ω:
T=2π1200≈6.28321200≈0.00524s
The frequency f is the reciprocal of the time period:
f=1T
Substituting the value of T:
f=10.00524≈191.0Hz
- Time Period T≈0.00524s
- Frequency f≈191.0Hz
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition ASSERTION REASON TYPE QUESTIONS
10 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Knowledge Check
The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2The maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
A(a) 0.01sB(b) 10sC(c ) 0.1sD(d) 100sThe ratio of the maximum velocity and maximum displacement of a particle executing simple harmonic motion is equal to
AωBTCgDn
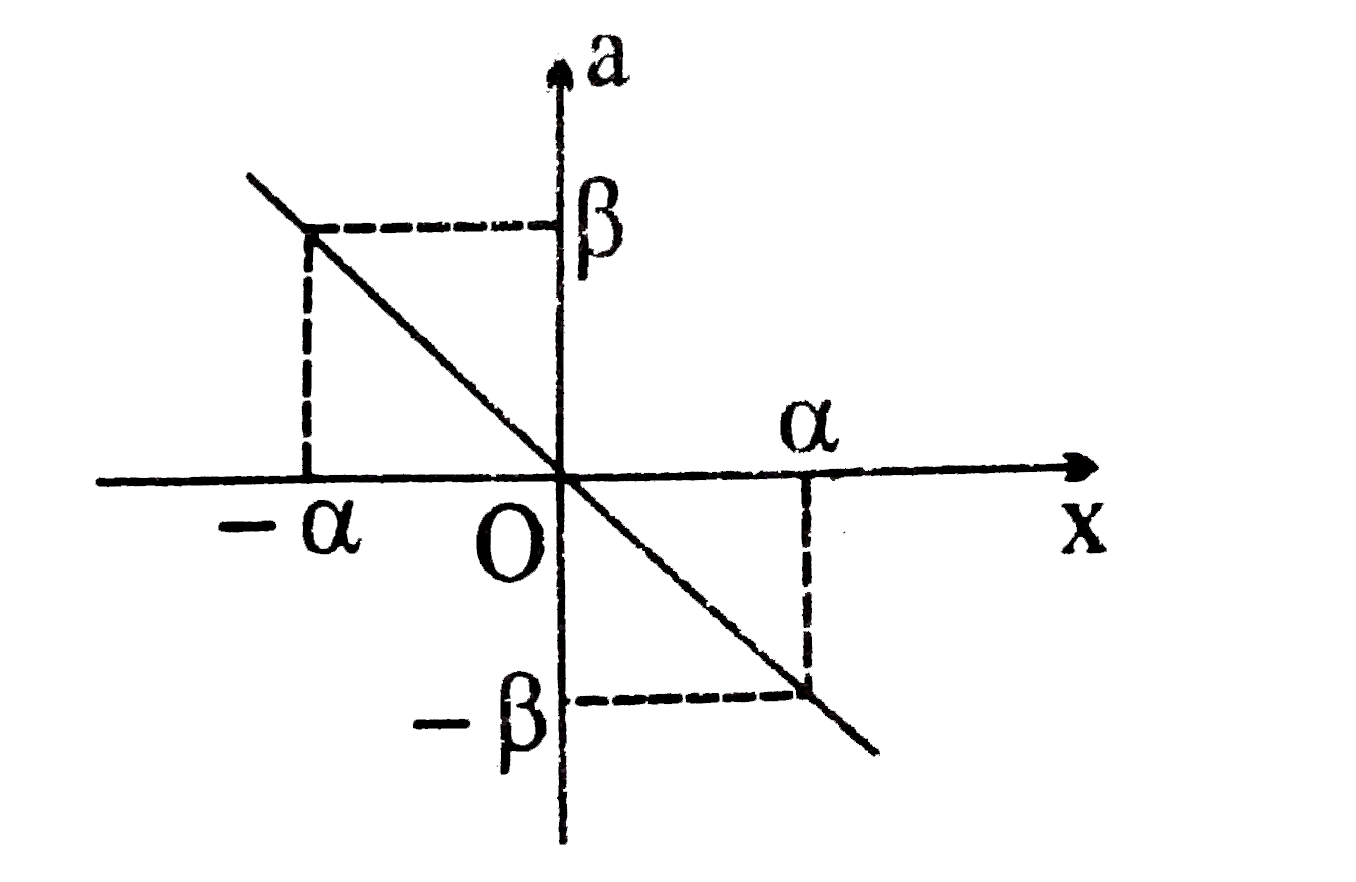
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.
View SolutionThe maimum velocity of a particle, executing SHM with an amplitude 7 mm is 4.4 m/s. the period of oscillation is
View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
View SolutionIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
View SolutionFor a particle executing simple harmonic motion, the amplitude is A and time period is T. The maximum speed will be
View Solution