(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
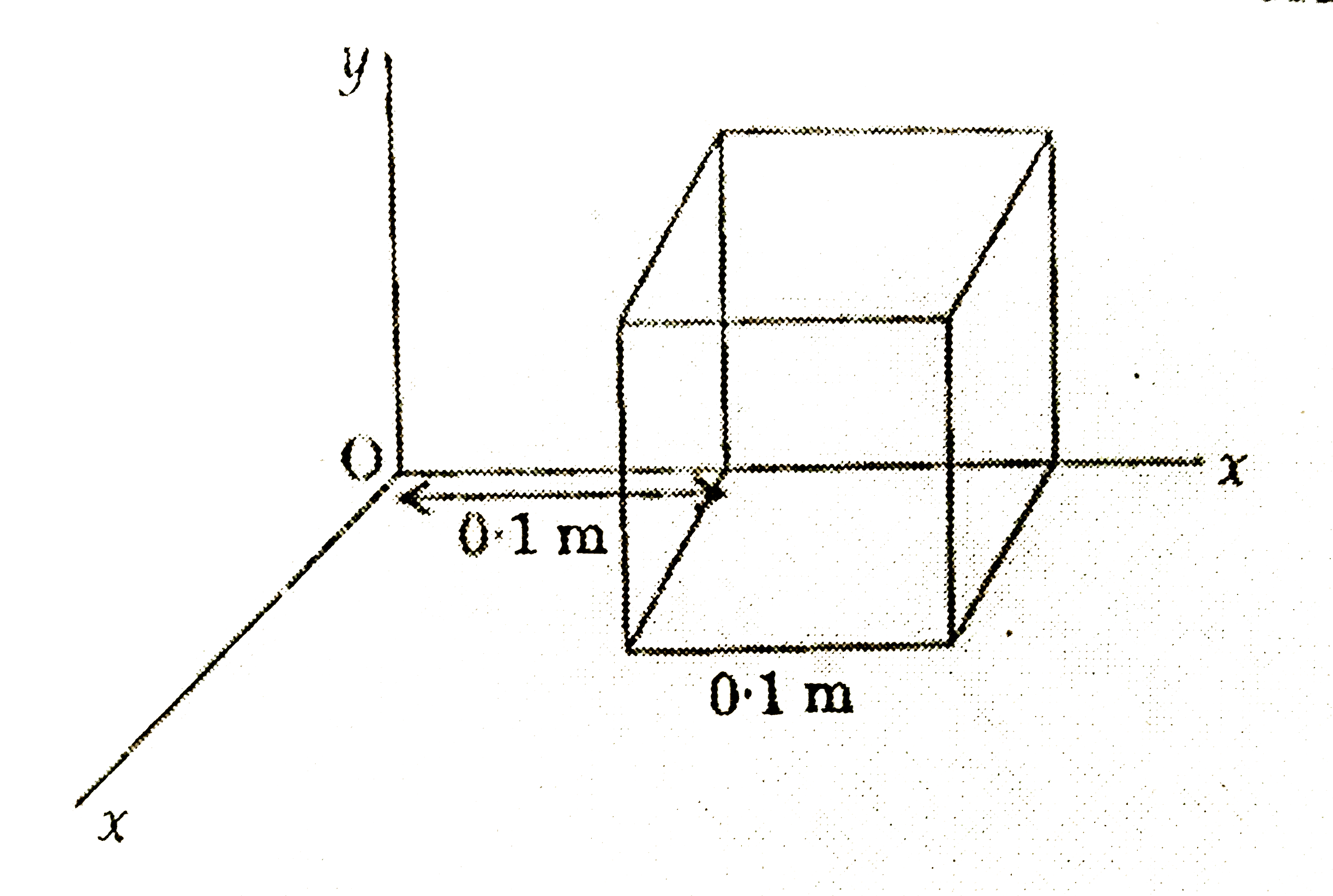
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
(a) Since the electric field has only an x component. For faces perpendicular to x direction, the angle between E and ΔS is ±π/2. Therefore the flux ϕ=E,ΔS is separately zero for each face of the cube except the two shaded ones. Now th magnitude of the electric the two shaded ones. Now the magnitude of the electric at the left face is
EL=ax3/2=aa1/2
(x=α at the left face)
The magnitude of electric field at the night face is
ER=ax1/2=α(2a)1/2
(x=2a at the right face).
The coresponding fluxes are
ϕL=EL,ΔS=ΔSEL.ˆnL=ELΔScosθ=−ELΔS,sinceθ=180∘=−ELa2
ϕR=ER.ΔS=ERΔScosθ=ERΔS,sinceθ=0∘=ERa2
Net flux through the cube
ϕR=ϕL=ERa2−ELa2=αa3[(2a)1/2−a1/2]
=αa5/2(√2−1)
=800(0.1)5/2(√2−1)
=1.05Nm2C−1
(b) We can use Gauss's law to find th total charge q inside the cube We have ϕ=q/ε0orq=ϕε0 therefore
q=1.05×8.854×10.−12C=9.27×10−12C..
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise34videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions32videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise17videos
ELECTROMAGNETIC INDUCTION
Similar Questions
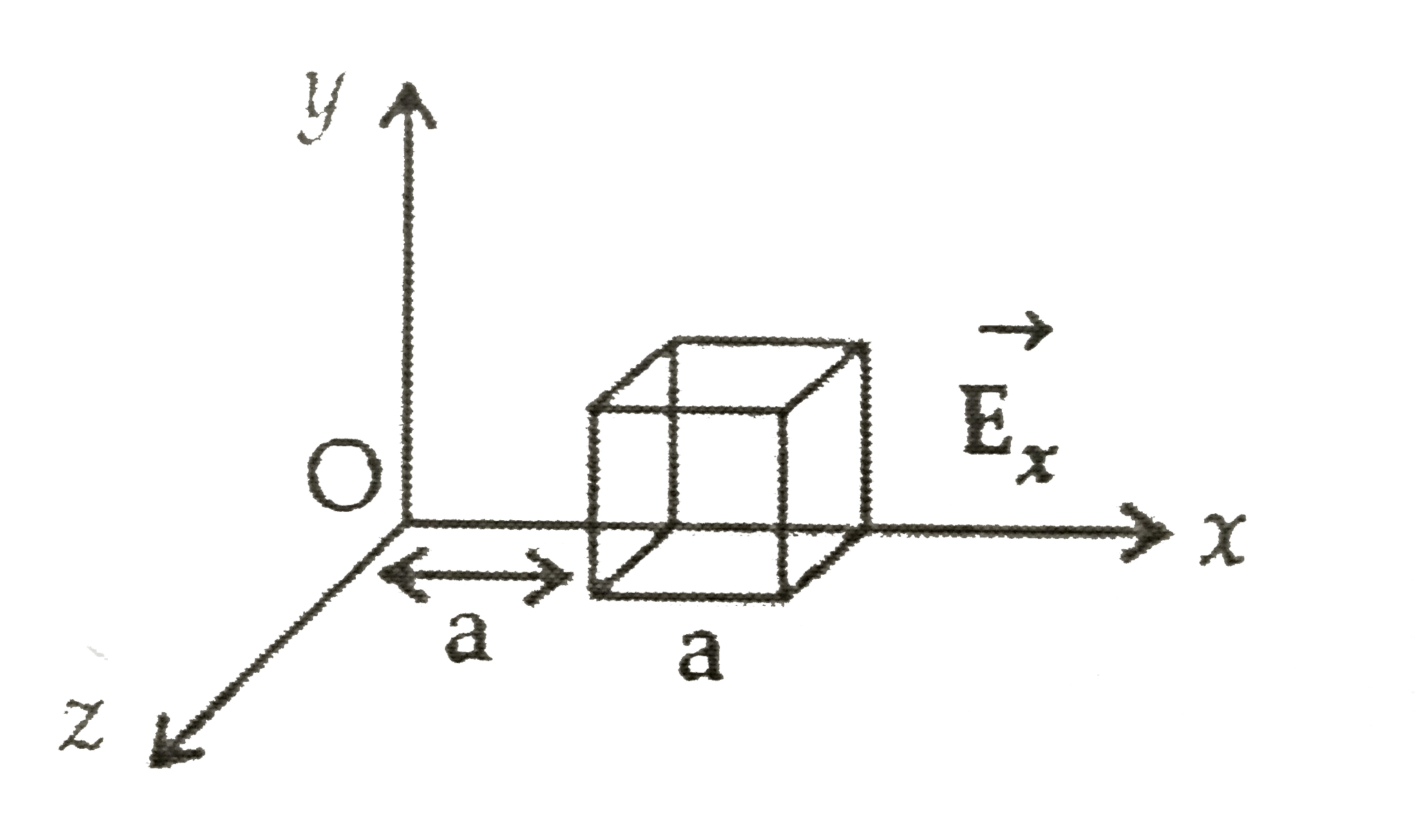
Define electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
 View Solution
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
 View Solution
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
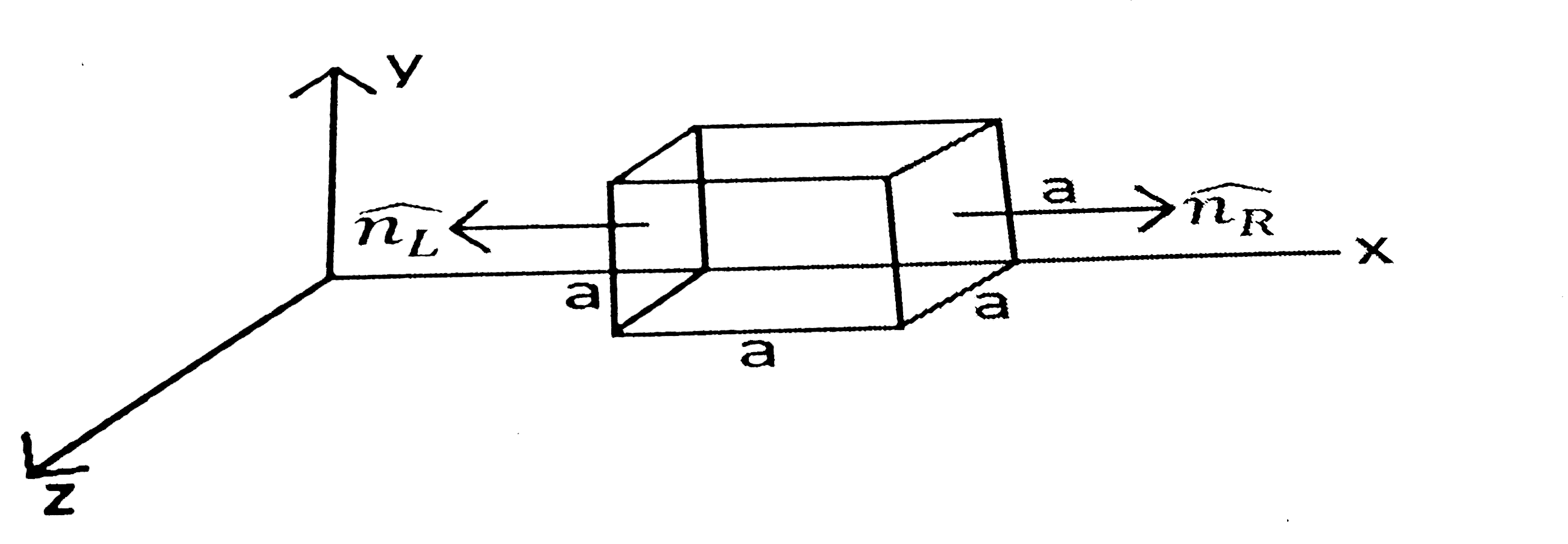
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
 View Solution
View Solution(a) Define electric flux. Write its S.I. units.
(b) Using Gauss's law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c ) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged ?View SolutionDefine the term .electric flux.. Write its SI units. What is the flux due to electric field →E=3×103ˆiN/C through a square of side 10 cm, when it is held normal to →E ?
View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
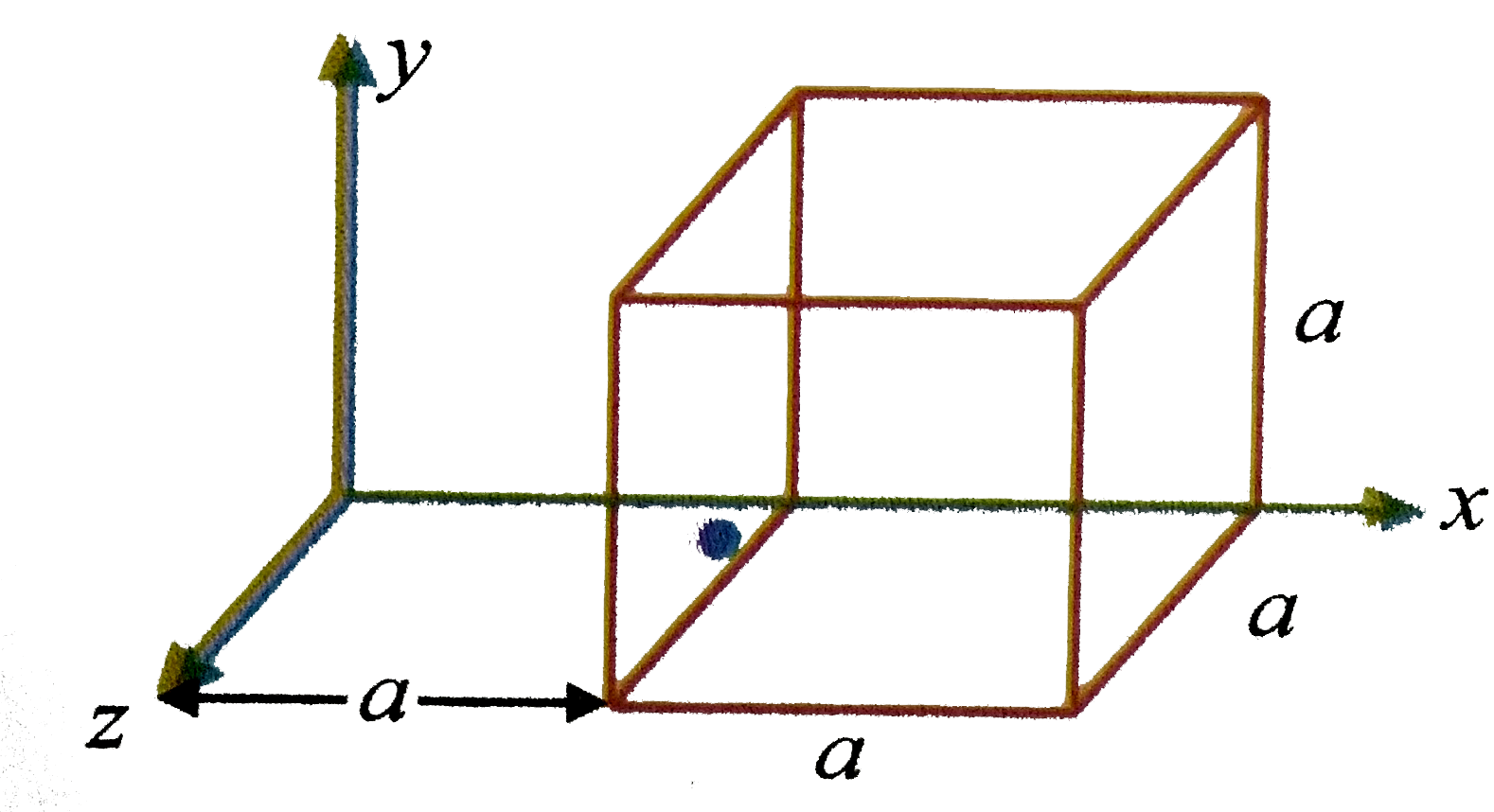 View Solution
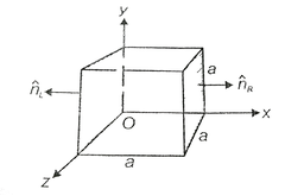
View SolutionState Gauss’s law in electrostatics. A cube with each side a is kept in an electric field given by E = Cx (as shown in the figure) where C is a positive dimensional constant. Find out :
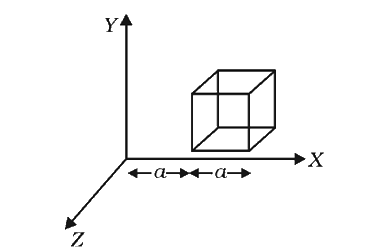
(i) The electric flux through the cube (ii) The net charge inside the cube.View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
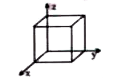 View Solution
View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. The charge enclosed in the cube of side 1m oriented as shown in the diagram is given by α∈0. Find the value of α.
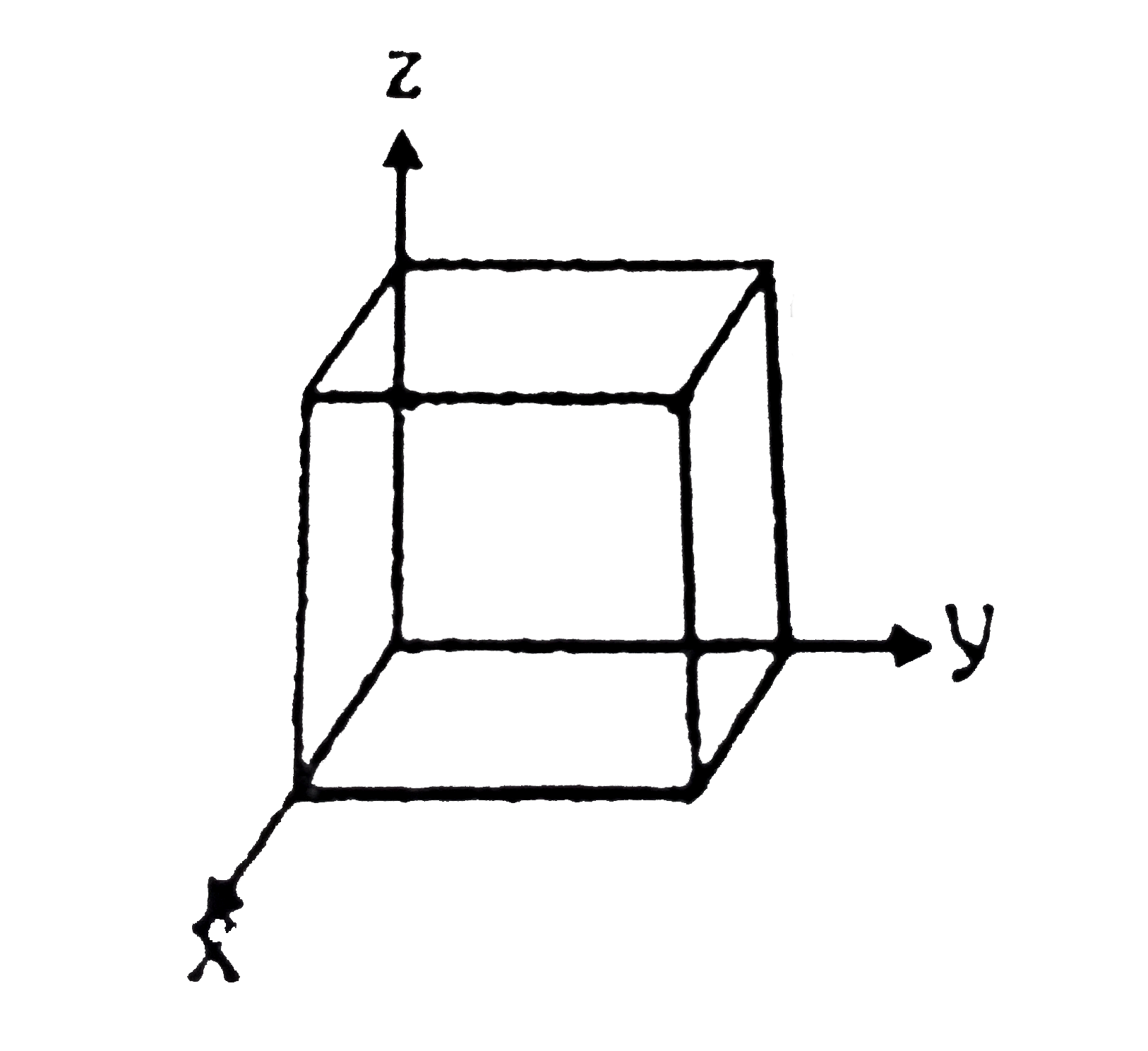 View Solution
View SolutionDue to a charge inside a cube the electric field is Ex=600x1/2,Ey=0,Ez=0. The charge inside the cube is (approximately):
 View Solution
View Solution

