(a) Define electric flux. Write its S.I. units.
(b) Using Gauss's law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c ) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged ?
(a) Electric flux is defined as the dot product of electric field intensity vector. Its S.I. unit is Nm2/C.
(b) Let σ be the uniform surface charge density of an infinite plane sheet. Consider a Gaussian surface to be a rectangular sectional area A.
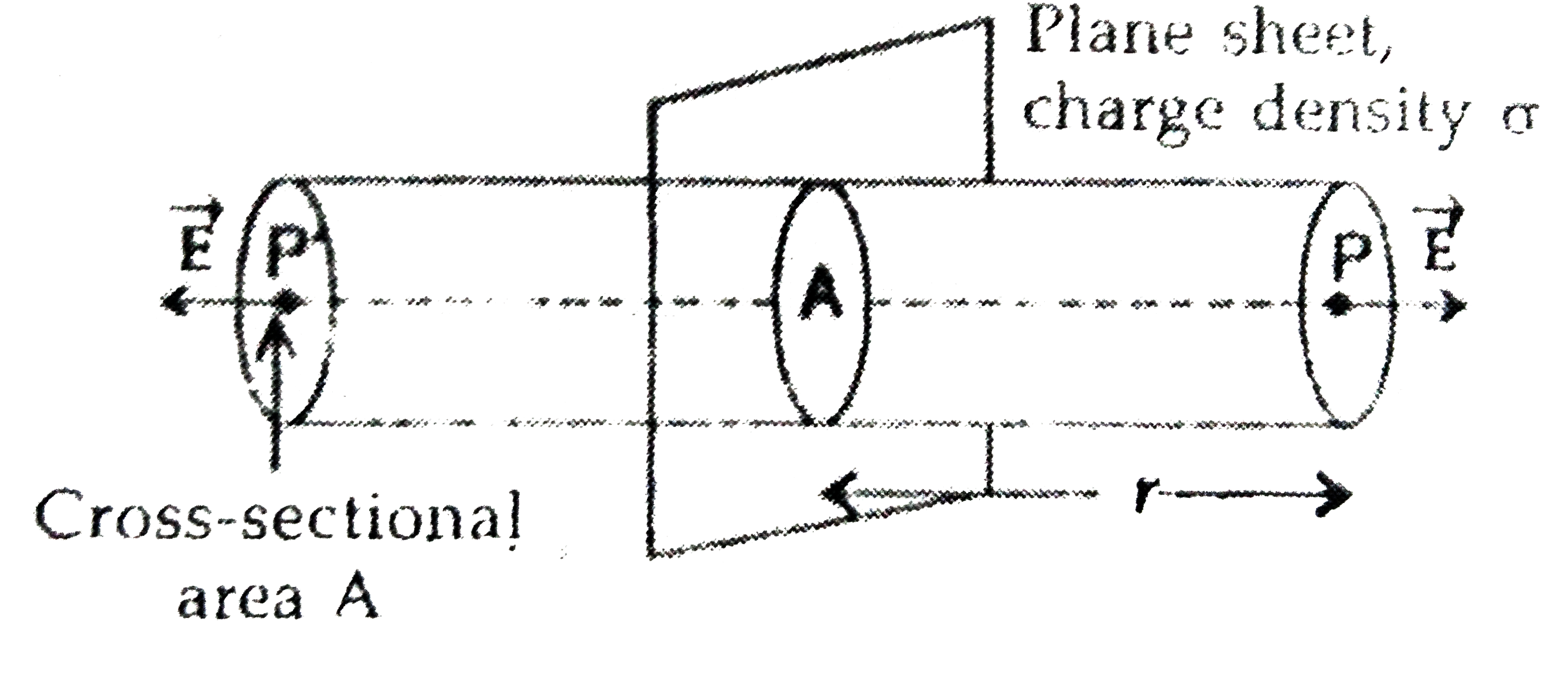
From figure, only the two faces 1 and 2 will contribute to flux. Electric field lines are parallel to the other faces and they do not contribute to the total flux.
The net flux through the Gaussian surface is 2EA. The charge enclosed by the closed surface is σA.
By Gauss's law, 2EA=σA∈0 or →E=σ2∈0ˆn
Since the expression does not contain x, so electric field is independent of the distance.
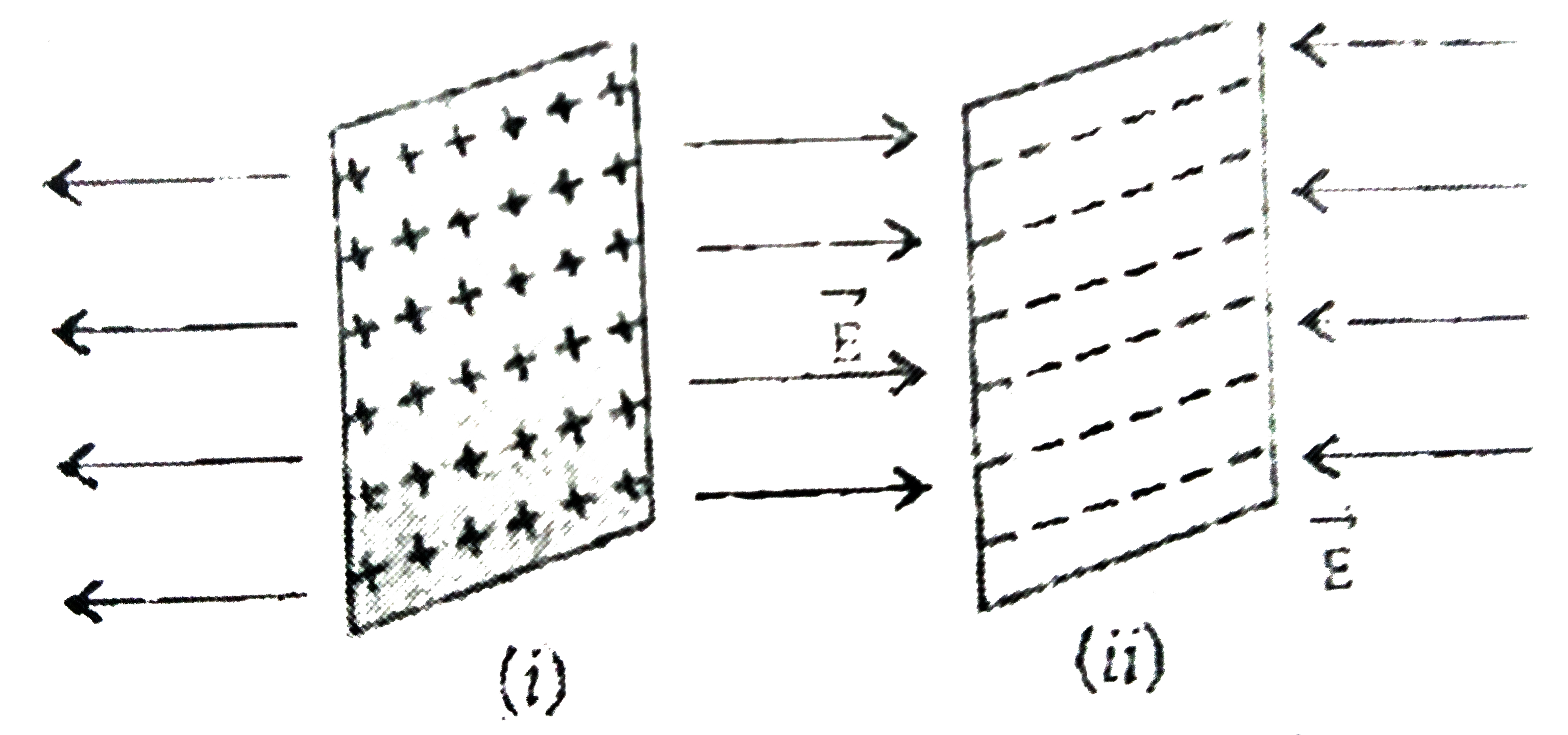
(c ) (i) The electric field is directed perpendicularly away from the sheet.
(ii) The electric field is directed perpendicularly towards the sheet.
Similar Questions
State Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionThe electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionThe ratio of distance of two satellites from the centre of earth is 1 : 4. The ratio of their time periods of rotation will be :
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionUse Gauss's law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities σ and −σ respectively.
View Solution

